Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.5 - Ex. 61
O suporte está soldado a ponto à extremidade do eixo no ponto . Para mostrar o efeito da força de sobre a solda, substitua a força por seu equivalente formado por uma força e um binário em . Expresse em notação vetorial.
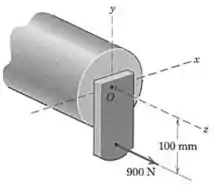
Passo 1
Vamos trocar a força por uma dupla formada por uma força e um binário em .
A nossa força vai ser simplesmente uma versão deslocada da força , de forma que seja aplicada exatamente sobre o ponto :
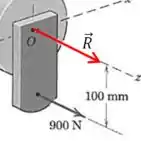
Passo 2
Agora precisamos encontrar um binário que corresponda ao momento gerado pela força na posição original.
Incialmente, o momento dessa força era:
Mas o enunciado pediu para representarmos . Como o suporte está soldado, a tendência da força é produzir uma rotação em torno do eixo :
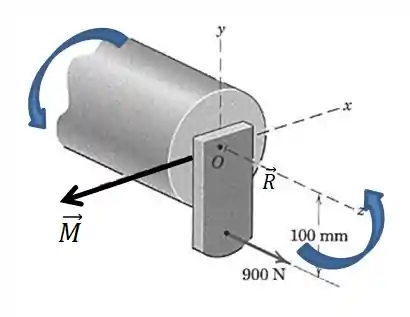
Você pode usar a regra da mão direita para definir a direção e sentido do vetor . Como já calculamos o módulo, podemos escrever:
Resposta
A força deve ser e o binário deve ser .