Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 14.Problemas - Ex. 28

14.28. Mostre que a Eq. (14.23) pode ser derivada diretamente da Eq. (14.11) substituindo por HO a expressão dada no Problema 14.27.

Passo 1

Vamos começar lembrando que equações são essas que o enunciado cita. A equação (14.11) é:

∑ M O = ∑ H ˙ O

A equação (14.23) é:

∑ M G = H ˙ G

E a expressão do problema 14.27 é:

H O = r - × m v - + H G

Passo 2

Nós podemos começar diferenciando H O = r - × m v - + H G

H O ˙ = r ˙ × m v - + r - × m v - ˙ + H G ˙

Mas sabemos que r ˙ = v e v ˙ = a

H O ˙ = v - × m v - + r - × m a - + H G ˙

Sabemos também que v - / / v - , então v - × m v - = 0

H O ˙ = r - × m a - + H G ˙

A segunda lei de Newton pode ser usada nesse problema também. ∑ F = m a - , logo

H O ˙ = r - × ∑ F + H G ˙

Dessa forma temos um lado da equação (14.11)

∑ M O = ∑ H ˙ O

∑ M O = r - × ∑ F + H G ˙

Passo 3

O outro lado da equação precisamos fazer uma analise mais geométrica.

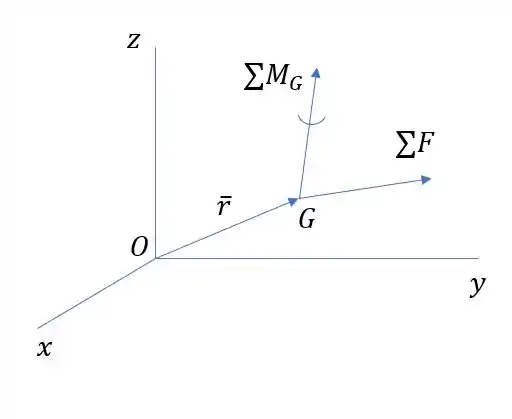
Podemos definir o ∑ M O como:

∑ M O = r - × ∑ F + ∑ M G

Substituindo isso na equação (14.11) temos:

r - × ∑ F + ∑ M G = r - × ∑ F + H G ˙

Agora podemos subtrair r - × ∑ F dos dois lados, finalmente chegamos em:

∑ M G = H G ˙

Que é exatamente a equação (14.23)

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na parte inferior de uma acrobacia aérea na qual o avião descreve um círculo no plano vertical x - y a uma altitude de 400m , o avião tem uma velocidade de 600k m / h sem aceleração horizontal x . O r
O dispositivo robótico do Prob. 2/162 agora gira em torno de um eixo vertical fixo enquanto seu braço é prolongado e elevado. Num determinado instante, ϕ = 30 ° , ϕ ˙ = 10g r a u s / s = c o n s t a n
A haste O A é mantida no ângulo constante β = 30 ° enquanto gira em torno do eixo vertical com uma velocidade angular constante θ ˙ = 120r p m . Simultaneamente, a esfera deslizante P oscila ao longo
No projeto de uma atração de parque de diversões, os carros são ligados a braços de comprimento R que são articulados a um anel central rotativo que impulsiona o conjunto em torno do eixo vertical com
A partícula P se desloca para baixo na trajetória espiral que está enrolada ao redor da superfície de um cone circular reto com raio de base b e altura h . O ângulo γ entre a tangente à curva em qualq