Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 31
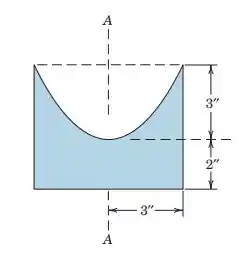
5.31. The figure represents a flat piece of sheet metal symmetrical about axis A-A and having a parabolic upper boundary. Choose your own coordinates and calculate the distance from the base to the center of gravity of the piece.
Passo 1
Vamos lá, queremos descobrir o centro de massa no eixo , e para isso vamos usar a equação
Primeiro vamos descobrir o elemento de área .
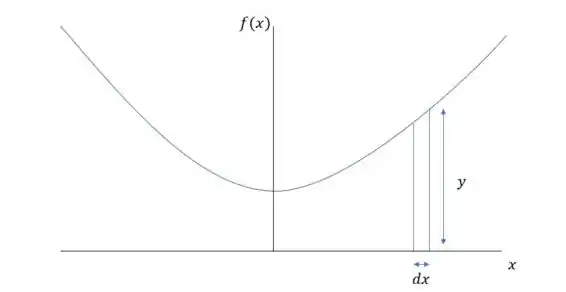
Então
E nessa imagem temos
Esse problema aqui tem uma simetria interessante para a gente, porque podemos resolver só para o lado direito do problema, em que , e assim a gente já consegue achar o ponto .
Passo 2
Pra continuar a resolução, vamos determinar a função . Bom, essa função é uma parábola, então é do tipo:
Para achar o valor de , vamos usar o ponto em que
Então
Agora para achar o valor de vamos calcular a função em um ponto qualquer, vamos usar e , então temos
Então
Ou
Então a função é
Passo 3
A única coisa que falta para montar a integral é a área da figura. A gente pode calcular a área usando:
Ou seja
Ou ainda
Essa integral fica
Passo 4
Agora a gente finalmente pode montar a nossa integral:
Isso fica
Substituindo o valor de
Podemos desenvolver esse quadrado
E isso fica
Então
E isso fica
E esse é o nosso ponto em do centro de massa.