Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas Fundamentais - Ex. 26

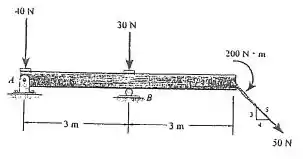
Substitua o carregamento do sistema por uma força e momento de binário resultante equivalente agindo no ponto .

Passo 1

Fala!

A questão pede para substituirmos todas as forças do problema por uma força resultante e um momento de binário resultante com relação ao ponto . A ideia é a gente calcular as resultantes da força e do momento em relação a causado por todas essas forcinhas.

Para isso, o primeiro passo é decompor as forças. Para nós usamos o triângulo dado para saber a orientação da força:

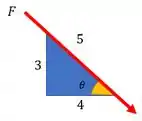
A componente é negativa porque a força aponta para baixo. A forma vetorial fica:

Desta forma, a força resultante:

Passo 2

Para o binário, basta calcular o momento de cada força com relação ao ponto e somar cada um. Lembrando a definição de momento:

O vetor , colocarmos nossa origem dos eixos em , vai ser a distância de cada linha de ação da força até . É só cê imaginar um vetor saindo de e indo até essa linha de ação. Para a inclinada:

Para a de :

Repara que colocamos porque as forças são paralelas a .

Além disso, temos um binário extra . Negativo porque está no sentido horário. Aí a gente o soma desse jeito mesmo ao outros para achar o momento resultante em .

Assim,

Somando todos os momentos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na posição em equilíbrio mostrada, a resultante das três forças atuando na haste dobrada passa pelo mancal O . Determine a força vertical P → . O resultado depende de θ ?

A polia e a correia em V presa a ela estão girando no sentido anti-horário e estão submetidas à carga de 1600N , devida aos dentes da engrenagem, e aos esforços trativos de 800N e 450N na correia em V

Para essa viga, as especificações de projeto para o encaixe em A dependem do módulo e da posição das cargas aplicadas. Represente a resultante das três forças e do momento por uma única força R → em A

Duas polias estão submetidas às forças trativas das correias, como mostrado. Se a resultante R → dessas forças passa pelo centro O , determine T → , o módulo de R → e o ângulo anti-horário θ que R → f

Determine a resultante R → das três forças atuando na treliça simples. Especifique os pontos sobre os eixos x e y através dos quais R → deve passar.