Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 147
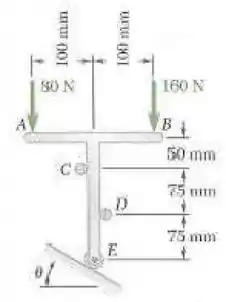
O suporte em forma de T mostrado na figura é apoiado por uma pequena roda em E e por cavilhas em C e D. despresando o efeito do atrito, determine (a) o menor valor de θ para que seu equilíbrio seja mantido, (b) as reações correspondentes em C, D e E.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Precisamos determinar o menor valor de para que haja equilíbrio, além das reações .
Olhando para a imagem do enunciado, podemos notar que todas as forças estão em (Newtons) e todas as medidas em mm (milímetros). Portanto não precisaremos fazer conversões.
Passo 2
O diagrama de corpo livre abaixo apresenta a representação das forças envolvidas.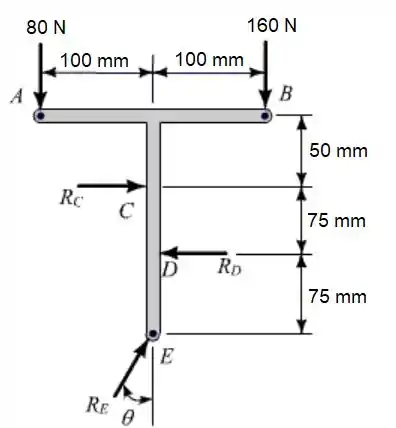
Como podemos observar, duas das reações procuradas atuam na horizontal e apenas uma possui componente horizontal (). Podemos encontrar a reação em função de .
Passo 3
Aplicaremos agora o momento em torno do ponto D:
=0
Substituindo a relação encontrada para no passo interior, encontraremos a relação de equilíbrio entre :
Pelo relação encontrada vemos que são diretamente proporcionais, como a função tan é crescente de 0 a . Nesse intervalo podemos afirmar que aumenta com o aumento de . Assim, o menor valor de é quando Assim:
Passo 4
Utilizando o valor de encontrado no passo 3 na relação encontrada no passo 2 podemos encontrar o valor de .
Finalmente, aplicamos o somatório das forças em x para encontrar a reação
O sinal positivo indica que o sentido da reação é o mesmo adotado no diagrama de corpo livre, ou seja, da direita para a esquerda.