A haste leve e as pequenas esferas vinculadas, cada uma de massa , são apresentadas na posição de equilíbrio, onde todas as quatro molas estão igualmente pré-comprimidas. Determine a frequência natural e o período para pequenas oscilações em torno do pino sem atrito.
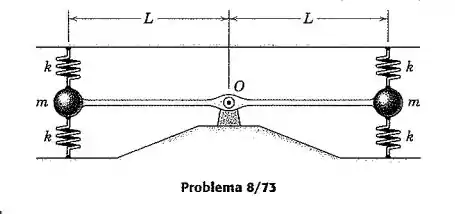
Passo 1
Para esse problema vamos usar as relações de torque resultante como também os conceitos de período e de frequência.
Passo 2
Vamos começar analisando o problema: temos que as forças que agem nesse sistema são as forças elásticas causadas pelas molas, sempre funcionando em pares, logo quando o sistema se move temos que o torque resultante será duas vezes a força aplicada. Assim, temos que
Onde é a distância vertical de onde está sendo aplicada a força. Como se trata de uma haste, temos que seu momento de inércia é . Portanto, temos que nossa equação fica
Para pequenos ângulos, temos que . Assim, ficamos com a equação da seguinte forma
Lembrando uma equação de um oscilador harmônico, onde sua equação é dada por . Sendo sua frequência dada por . Logo, por ser similar, temos que nossa frequência será
Passo 3
Temos que o período é dado por . Assim, temos que nosso período será