Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 41
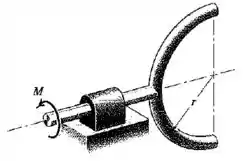
A metade de um anel de massa e raio está soldada a um pequeno eixo horizontal montado em um mancal conforme apresentado. Despreze a massa do eixo e determine a aceleração angular do anel quando um torque é aplicado ao eixo.
Passo 1
O momento de inércia de um anel (inteiro) de massa em torno de um eixo como esse da figura seria:
Como o momento de inércia é um somatório (e, no limite, uma integral):
O fato de que excluímos alguns pedaços (transformamos em massa ) não muda a forma geral da equação, apenas então o momento de inércia desse meio-anel de massa será:
E se tivéssemos um anel completo, seria simplesmente:
Passo 2
Então para um momento aplicado sobre esse anel, a aceleração angular gerada seria:
Resposta
A aceleração angular do anel é .
Exercícios de Livros Relacionados
A viga AE de 2,5m está sendo baixada por dois guindastes. No instante mostrado na figura, sabe-se que a velocidade do ponto D é de 600m m / s para baixo e que a velocidade do ponto E é de 900m m / s p
Um helicóptero desloca-se horizontalmente na direção x a uma velocidade de 200k m / h . Sabendo que as lâminas principais giram no sentido horário com uma velocidade angular de 180r p m , determine o
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 750m m / s . Sabendo que o carretel de 80 mm de raio tem uma velocidade angular de 15r a d / s no sentido hor
O carretel de fita e sua estrutura de apoio são puxados para cima com uma velocidade v A = 100m m / s . Sabendo que a extremidade B da fita é puxada para baixo com velocidade de 300m m / s e que, no i
Resolva o Problema Resolvido 15.2, considerando que a cremalheira inferior não é fixa, mas se desloca para a esquerda com velocidade de 0,6m / s .