Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 83

Um vagão ferroviário tem massa 30   M g e é apoiado em oito rodas de 800   m m de diâmetro, com eixos de 125   m m de diâmetro. Sabendo que os coeficientes de atrito são μ s = 0,020 e μ k = 0,015 , determine a força horizontal necessária a para movimento iminente do vagão, b para manter o vagão movendo-se em velocidade constante. Despreze a resistência ao rolamento entre as rodas e os trilhos.

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Bom pessoal, primeiro vamos imaginar aa seguinte situação:

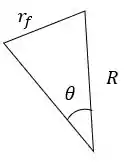
Teremos então que:

tan ⁡ θ = r f R

Como r f = r ⋅ μ , teremos que:

tan ⁡ θ = r ⋅ μ R

Passo 2

Agora, vamos calcular a relação entre a força e o peso. Temos que:

F = W ⋅ tan ⁡ θ

Ou seja:

F = W ⋅ r ⋅ μ R

Substituindo os raios, temos que:

F = W ⋅ μ ⋅ 62,5 400

F = 0,15625 ⋅ W ⋅ μ

Passo 3

Agora, vamos calcular a somatória do peso para oito rodas do vagão:

∑ F = 8 ⋅ 0,15625 ⋅ W ⋅ μ

∑ F = 8 ⋅ 0,15625 ⋅ 30   M g ⋅ 9,81 ⋅ μ

∑ F = 45,984 ⋅ μ   k N

Observe que deixei em função de μ justamente para só substituirmos o determinado μ para cada situação.

Passo 4

Para o item a, vamos utilizar o μ s , que é o coeficiente de atrito estático.

∑ F = 45,984 ⋅ 0,020   k N

∑ F = 0,9197   k N

Para o item b, vamos utilizar o μ k , que é o coeficiente de atrito cinético.

∑ F = 45,984 ⋅ 0,0 15   k N

∑ F = 0 , 6897   k N

Resposta

a )   ∑ F = 0,9197   k N

b )   ∑ F = 0,6897   k N

θ m = 29,7 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um dispositivo de segurança utilizado por trabalhadores que sobem escadas fixas em estruturas de grande altura consiste em um trilho preso à escada que pode deslizar na flange do trilho. Uma corrente
Uma alavanca de peso desprezível é montada com folga em um eixo de 30m m de raio mostrado na figura. Sabendo que a aplicação da força P de intensidade 275N irá justamente iniciar a rotação no sentido
O binário M B é aplicado no giro do tambor motriz para manter a velocidade constante da cinta de polimento mostrada na figura. Sabendo que μ k = 0,45 entre a cinta e o bloco de 15k g , inicia o polime
Um base máquina de 900k g é rolada ao longo de um piso de concreto usando uma série de tubos de aços com diâmetro externo de 100m m . Sabendo que o coeficiente de resistência ao rolamente é 0,5m m ent
O elo de ligação mostrado na figura é usado frequentemente na construção de pontes de rodovias para possibilitar a expansão causada por variações de temperatura. Em cada um dos pinos A e B de 60m m ,