Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 13
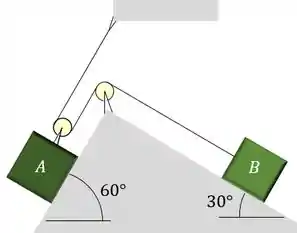
Determine a velocidade do bloco de 30 kg se os dois blocos são soltos do repouso e o bloco de 20 kg se desloca 0,6 m subindo o plano inclinado. O coeficiente de atrito cinético entre ambos os blocos e os planos inclinados é de .
Passo 1
O enunciado nos dá as seguintes informações:
Massa do bloco : ;
Massa do bloco : ;
Deslocamento de : ;
Coeficiente de atrito: .
Os dois blocos partem do repouso, logo
Deevemos determinar a velocidade do bloco após o bloco se deslocar 0,6 m.
Primeiramente, vamos desenhar o diagrama de corpo livre de cada bloco.
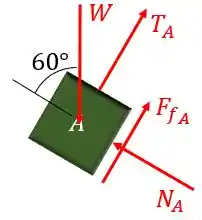
Onde é a força peso, é a força de atrito, é a força normal e é a força exercida pelo cabo.
Como os dois bloco são puxados pelo mesmo cabo, temos que
Uma vez que do bloco , saem dois cabos devido a polia existente.
Passo 2
Inicialmente, vamos aplicar a equação do movimento.
No bloco :
Em :
Logo,
No bloco :
Em :
Logo,
Passo 3
Agora vamos aplicar o Princípio do Trabalho e Energia.
Vemos que tanto a força peso quando a força de atrito realizam trabalho sobre os blocos.
A força nao realiza trabalho, pois ela representa as reações nos apoios e, por esse motivo, ela não se move enquanto os blocos são deslocados. A força normal também não realiza trabalho pois não atua na direção do movimento.
Sabemos que
Logo,
Lembre-se de que o trabalho é positivo quando o componente da força está no mesmo sentido de direção que o seu deslocamento. Caso contrário, ele é negativo.
Substituindo os valores se , e , obtemos
Passo 4
Utilizando os métodos da cinemática, podemos ver na Figura dada pela questão que o comprimento total de todos os seguimentos verticais do cabo pode ser expresso como
Logo, uma variação na posição dos blocos resulta na seguinte equação de deslocamento:
Vemos que um deslocamento para baixo de um bloco produz um deslocamento para cima do outro bloco, o que faz sentido ao imaginar a situação dada pela questão.
Portanto, quando m, temos que m.
Além disso, sabemos que a velocidade é dada pela variação de espaço em um intervalo de tempo, logo, a derivada temporal da seguinte equação de resulta em
Passo 5
Substituindo os valores de , e na equação abaixo, obtemos