Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.6 - Ex. 120
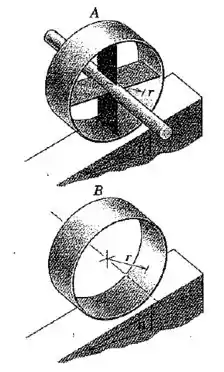
As duas rodas do Prob. 6/82, mostradas aqui novamente, representam duas condições extremas de distribuição de massa. Para o caso toda a massa é assumida como sendo concentrada no centro do aro, na barra axial de diâmetro desprezível. Para o caso toda a massa é assumida como sendo concentrada no aro. Determine a velocidade do centro de cada aro, após ter se deslocado uma distância para baixo na inclinação a partir do repouso. Os aros rolam sem deslizar.
Passo 1
Nos dois casos, o fenômeno é o mesmo. O aro parte do repouso () e, conforme desce, sua energia potencial gravitacional é convertida em energia cinética:
A energia cinética total pode ser escrita como a soma das energias de translação e rotação:
E a variação da energia potencial gravitacional pode ser escrita da seguinte forma:
Então:
Passo 2
Agora vamos analisar cada caso separadamente. No caso , como toda a massa está concentrada no centro, teremos:
Então:
E no caso temos que usar a expressão para o momento de inércia de um aro:
E também vamos reescrever a velocidade angular como :
Resposta
As velocidades serão e .