Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 19
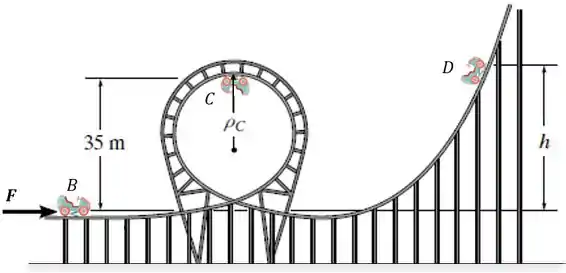
Determine a altura da rampa que o carrinho da montanha-russa de 200 kg atingirá se for lançado em com uma velocidade apenas suficiente para dar a volta no topo do loop em sem deixar os trilhos. O raio de curvatura em é m.
Passo 1
O enunciado nos deu as seguintes informações:
Massa do carrinho: ;
Raio de curvatura em : .
O carrinho deve ser lançado com velocidade apenas suficiente para realizar o loop em . Isso nos diz que, em , o carrinho estará na iminência de perder contato com a pista e que, neste ponto, a força normal tenderá à zero. Logo, podemos considerar que neste ponto.
Devemos detrminar a velocidade de lançamento do carrinho para que ele atenda essa restrição.
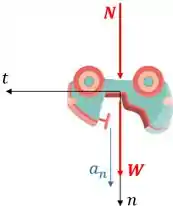
Inicialmente, desenhamos o diagrama de corpo livre do carrinho:
Passo 2
Aplicando a Equação de Movimento, temos
No eixo
Sabemos que , logo
Passo 3
Agora, vamos aplicar o Princípio do Trabalho e Energia.
Entre os ponto e :
Temos que
Logo,
O trabalho realizado é negativo pois no trajeto o sentido da força peso é oposto ao deslocamento do carrinho.
Substituindo os valores na equação inicial, obtemos
Entre os pontos e :
Em , a velocidade do carrinho será igual à zero, pois neste ponto, queremos descobrir a altura máxima que ele atingiria.
Temos que
Logo,
Aqui, o trabalho realizado também é negativo pois a força peso atua no sentido oposto ao deslocamento .
Substituindo os valores na equação inicial, obtemos