Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 20.Problemas - Ex. 8

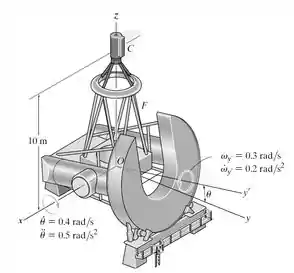
O telescópio está montado sobre uma estrutura F que permite ser direcionado para qualquer ponto do céu. No instante θ = 30 ° , a estrutura tem uma aceleração   α   y = 0,2   r a d / s 2 e uma velocidade angular w y = 0,3   r a d / s em torno de y ' , e θ ¨ = 0,5   r a d / s 2 enqunto θ ˙ = 0,4   r a d / s . Determine a velocidade e a aceleração da cápsula de observação em C nesse instante.

Passo 1

A velocidade angular neste instante é:

ω = θ ˙ + ω y ' = - 0,4 i + ( 0,3 cos ⁡ 30 ° j + 0,3 sin ⁡ 30 ° k )

ω = [ - 0,4 i   +   0,2598 j   +   0,15 k ]

Passo 2

Observa-se que   ω y ' tem uma direção constante em relação ao sistema xyz rotativo que gira em Ω = θ ˙ = - 0,4   i     r a d / s . Com ( ω ˙ y ' ) x y z = α y ' =   0,2   c o s   30 ° j   +   0,2   s i n   30 ° k = 0,1732 j   +   0,1 k   r a d / s 2 .

ω ˙ y ' = ω ˙ y ' x y z + Ω × ω y '

ω ˙ y ' = 0,1732 j   +   0,1 k + ( - 0,4   i ) × ( 0,3 cos ⁡ 30 ° j + 0,3 sin ⁡ 30 ° k )

ω ˙ y ' = [ 0,2332 j   -   0,003923 k ]   r a d / s 2

Como θ ˙ é sempre direcionado no eixo X , onde Ω = 0 , então :

θ ¨ = ( θ ¨ ) x y z + Ω × θ ˙ = ( θ ¨ ) x y z + 0 × θ ˙ = [ - 0,5 i ] r a d / s 2

A aceleração angular será:

α = ω ˙ y ' + θ ¨ = - 0,5 i   +   0,2332 j   -   0,003923 k r a d / s 2

Passo 3

Velocidade e aceleração escalares:

v C = ω × r O C = ( - 0,4 i   +   0,2598 j   +   0,15 k ) × ( 10 k )

v C = 2.60 i   +   4.00 j m / s

a C = α × r O C + ω × ( ω × r O C )

a C = ( - 0,5 i   +   0,2332 j   -   0,003923 k ) × ( 10 k ) +(   - 0,4 i   +   0,2598 j   +   0,15 k ) × [(   - 0,4 i   +   0,2598 j   +   0,15 k ) × ( 10 k ) ]

a C = 1,73 i   +   5,39 j   -   2,275 k m / s 2

Resposta

De acordo com os passos 1, 2 e 3 a velocidade e a aceleração na cápsula de observação em C serão respectivamente :

v C = 2.60 i   +   4.00 j m / s

a C = 1,73 i   +   5,39 j   -   2,275 k m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A manivela AO gira no sentido horário com uma velocidade angular constante de 10 rad/s dentro de um arco limitado de seu movimento. Para a posição θ = 30 ° determine a velocidade angular da barra ranh
O ônibus espacial A está em uma órbita circular equatorial de 240 km de altitude e está se movendo de oeste para leste. Determine a velocidade e a aceleração que ele parece ter para um observador B fi
Determine a aceleração angular da haste EC na posição mostrada, onde ω = β ˙ = 2 r a d seβ ¨ = 6r a d / s 2 quando θ = β = 60 ° . O pino A é fixo na haste EC. A ranhura circular no elemento DO tem um
Dois satélites estão em orbitas circulares equatoriais de diferentes altitudes. O satélite A está em uma órbita geossíncrona (uma com o mesmo período que o da rotação da Terra, de modo que ele “paira”
A figura mostra as pás do impelidor de uma bomba centrífuga que gira com uma velocidade constante no sentido horário de 200 rpm. As partículas de fluido possuem uma velocidade absoluta cuja componente