Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 49
Um teste de vibrações é realizado para verificar a adequação do projeto dos mancais e . O rotor desbalanceado e o eixo incorporado possuem uma massa combinada de . Para determinar a posição do centro de massa, um torque de é aplicado ao eixo para mantê-lo em equilibrio em uma posição a da posição mostrada. Um torque constante é então aplicado ao eixo, que atinge uma velocidade de em rotação a partir do repouso. (Em cada rotação a aceleração angular varia, mas seu valor médio é o mesmo que para a aceleração constante.) Determine (a) o raio de giração do rotor e do eixo em relação ao eixo de rotação, (b) a força que cada mancal exerce sobre o eixo imediatamente após ser aplicado, e (c) a força exercida por cada mancal quando a velocidade de é atingida e é removido. Despreze qualquer resistência relativa ao atrito e as forças no mancal devidas ao equilíbrio estático.
Passo 1
O eixo atinge uma velocidade de em rotações a partir do repouso. Podemos usar essa informação para calcular a aceleração angular média:
Então:
Passo 2
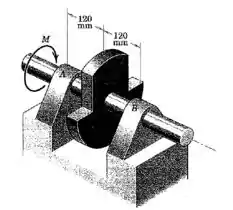
Outra informação que podemos tirar do enunciado é a posição do centro de massa. O eixo fica em equilíbrio em uma posição a da mostrada na figura, quando um torque é aplicado.
Isso quer dizer que esse torque é suficiente para compensar o torque da força peso do rotor e do eixo, e assim manter o equilíbrio:
Onde é a distância entre o centro de masssa do rotor e o eixo que passa pelos mancais:
Passo 3
(a) Ok, agora vamos calcular o que foi pedido. Primeiro queremos o raio de giração do rotor e do eixo, em relação ao eixo de rotação.
Nós vimos que um momento de produziu uma aceleração angular , então:
Mas podemos reescrever o momento de inércia em função do raio de giração:
Passo 4
(b) Quando o sistema se move com aceleração angular , qual a aceleração tangencial do centro de massa?
Nós já calculamos que a distância do centro de massa até o eixo é , então:
E as únicas forças que agem na direção tangencial (imediatamente após a aplicação do momento) são as forças horizontais em cada mancal:
Passo 5
(c) Quando o mancal atinge uma velocidade angular de , e o momento deixa de ser aplicado, o sistema não tem mais aceleração tangencial.
Entretanto, como o eixo mantém a trajetória circular, e portanto ainda há uma resultante produzindo aceleração centrípeta:
Essa resultante é justamente a soma da força exercida por cada mancal:
Onde é a aceleração centrípeta do centro de massa, então esse raio é a distância que calculamos antes:
Resposta
(a) .
(b) .
(c) .