O sistema do Prob. 8/46 é repetido aqui. Se a barra curva possui agora uma massa e um raio de giração em relação ao ponto , determine expressões para a frequência natural não amortecida e para o fator de amortecimento em termos das propriedades conhecidas do sistema. Assuma pequenas oscilações. O coeficiente de amortecimento para o amortecedor é .
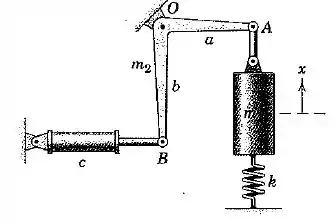
Passo 1
Vamos supôr que a barra sofra uma pequena oscilação em torno de , de forma que o ponto suba um pouco e o ponto desça um pouco:
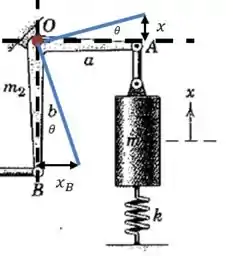
Usando a tangente do ângulo podemos escrever uma relação entre os deslocamentos:
E para o ângulo :
Essas relações são importantes para podermos escrever a equação de movimento em relação a .
Passo 2
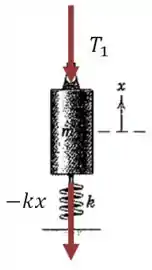
Agora vamos olhar para as forças que agem sobre o cilindro na vertical (que se move ao longo do eixo que o enuncaido resolveu chamar de ):
Quando vemos um pequeno deslocamento do cilindro, as forças que agem sobre ele são as seguintes:
E agora vamos olhar para barra curva :
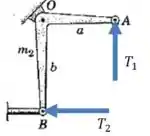
E podemos aplicar uma equação de momentos em torno do ponto :
E a força que aparece em está ligada com compressor que tem constante de amortecimento :
Passo 3
Então ficamos com o seguinte sistema:
Agora podemos aproveitar as relação que escrevemos no primeiro passo para substituir e :
Vamos multiplicar a segunda equação por e somar com a primeira:
Agora vamos dividir tudo por e reorganizar a equação:
E essa é a equação de movimento que estávamos procurando.
Passo 4
Então ficamos com o seguinte sistema. Vamos comparar com a equação geral para o oscilador:
Então a frequência de oscilação é:
E o fator de amortecimento é:
Resposta
A frequência natural é e o fator de amortecimento é .