Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 110
Se está no centro da face do sólido retangular, expresse como um vetor em termos dos vetores unitários , e . Determine a projeção escalar de ao longo da linha . Os valores de , , e são conhecidos.
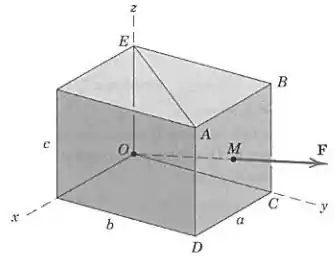
Passo 1
Podemos escrever assim:
onde é o vetor unitário que sai de em direção a , ou seja, na mesma direção e sentido de :
Passo 2
Podemos determinar a projeção escalar da força ao longo da linha calculando o produto escalar entre o vetor que acabamos de obter e o vetor unitário , que sai de em direção a :
Resposta
Exercícios de Livros Relacionados
Dois cabos são usados para segurar o mastro guincho na posição e sustentar a carga de 1500 N. Se a força resultante é direcionada ao longo do mastro do ponto A para O , determine os valores de x e z p
O cabo conectado aos mastros de uma grua exerce uma força sobre a grua de F = 1,75 kN. Expresse essa força como um vetor cartesiano.
A chapa cilíndrica está submetida às três forças dos cabos que são concorrentes no ponto D . Expresse cada força que os cabos exercem na chapa como um vetor cartesiano e determine a intensidade e os â
Uma força de F = 80N é aplicada no cabo da chave. Determine o ângulo θ entre a origem da força e o cabo da chave A B .
Determine as intensidades das componentes projetadas da força F = 300N que atuam ao longo dos eixos x e y .