Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 61

Um vagão do metrô parte da estação A e ganha velocidade à razão de 2 m / s ² por 6 s e, depois, à razão de 3 m / s ² até alcançar a velocidade de 24 m / s . O carro mantém a velocidade até aproximar-se da estação B; os freios são aplicados, dando ao carro uma desaceleração constante e levando-o a parar em 6 s . O tempo total do percurso de A a B é de 40 s . Desenhes as curvas a - t ,   v - t   e   x - t e determina a distância entre as estações A e B.

Passo 1

O enunciado pede para a gente determinar a distância entre as estações A e B.

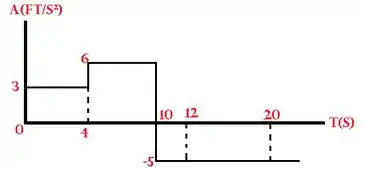
  1. Condições iniciais: t = 0 ,   v 0 = - 18 f t / s ,   x 0 = 0

    Mudança em v é igual à área sob a - t curve:

    v 0 = - 18 f t / s

    0 < t < 4 s : v 4 - v 0 = ( 3 f t / s ² )   x   ( 4 s ) = + 12 f t / s v 4 = - 6 f t / s

    4 s < t < 10 s : v 10 - v 4 = ( 6 f t / s ² )   x   ( 6 s ) = + 36 f t / s v 10 = + 30 f t / s

    10 s < t < 12 s : v 12 - v 10 = ( - 5 f t / s ² )   x   ( 2 s ) = - 10 f t / s v 12 = + 20 f t / s

    12 s < t < 20 s : v 20 - v 12 = ( - 5 f t / s ² )   x   ( 8 s ) = - 40 f t / s v 20 = - 20 f t / s

    Passo 2

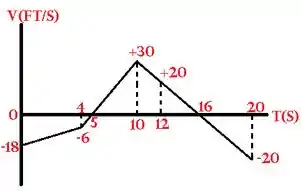
    Mudança em x é igual à área sob v - t curve:

    x 0 = 0

    0 < t < 4 s : x 4 - x 0 = 1 2   x   - 18 - 6   x   4 = - 48 f t x 4 = - 48 f t

    4 s < t < 5 s : x 5 - x 4 = 1 2   x   - 6   x   1 = - 3 f t x 5 = - 51 f t

    5 s < t < 10 s : x 10 - x 5 = 1 2   x   + 30 x   5 = + 75 f t x 10 = + 24 f t

    12 s < t < 10 s : x 12 - x 10 = 1 2   x   + 30 + 20   x   2 = + 50 f t x 12 = + 74 f t

    16 s < t < 12 s : x 16 - x 12 = 1 2   x   + 20 x   4 = + 40 f t x 16 = + 114 f t

    20 s < t < 16 s : x 20 - x 16 = 1 2   x   ( - 20 )   x   ( 4 ) = - 40 f t x 20 = + 74 f t

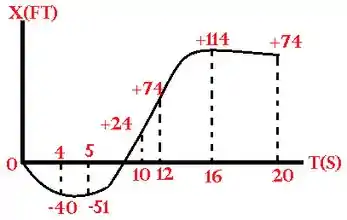
  2. Das curvas acima, lemos:

Para t = 12 s : v 12 = + 20 f t / s , x 12 = + 74 f t

Distância viajada t = 0 para t = 12 s

A partir de t = 0 s para t = 5 s : distância viajada = 51 f t

A partir de t = 5 s para t = 12 s : distância viajada = 51 + 74 = 125 f t

Resposta

  1. 10 s < t < 12 s : v 12 - v 10 = ( - 5 f t / s ² )   x   ( 2 s ) = - 10 f t / s v 12 = + 20 f t / s

    2. 12 s < t < 10 s : x 12 - x 10 = 1 2   x   + 30 + 20   x   2 = + 50 f t x 12 = + 74 f t

  2. Para t = 12 s : v 12 = + 20 f t / s , x 12 = + 74 f t

Distância total percorrida = 176 f t

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Os carros de corrida A e B se deslocam em trechos circulares de um autódromo. No instante mostrado na figura, a velocidade de A está decrescendo a uma taxa de 7 m/s² e a velocidade de B está aumentand
Um projétil é disparado a partir do ponto A com uma velocidade inicial v0 que forma um ângulo α com a horizontal. Expresse o raio de curvatura da trajetória do projétil no ponto C em termos de x, v0,
O carvão é descarregado da carroceria de um caminhão basculante com uma velocidade inicial de vA = 2 m/s ∡ 50°. Determine o raio de curvatura da trajetória descrita pelo carvão (a) no ponto A, (b) no
Uma partícula se move ao longo da espiral mostrada na figura. Determine a intensidade da velocidade da partícula em termos de b, θ , θ ˙ .
Determine o raio de curvatura da trajetória descrita pela partícula do Problema 11.95 quando t = 0.