Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 42
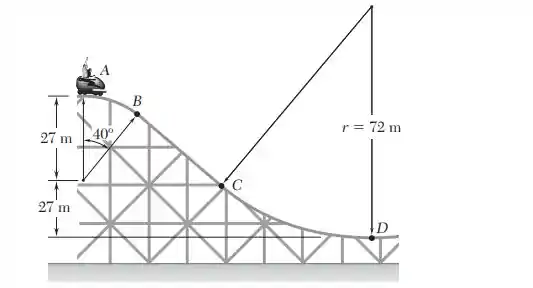
Um trecho da pista de uma montanha-russa consiste de dois arcos de círculo e unidos por um trecho reto . O raio de é 27 m e o raio de é 72 m. O carrinho e seus ocupantes, de massa total de 280 kg, alcançam o ponto praticamente sem velocidade e então caem livremente ao longo da pista. Determine os valores máximo e mínimo da força normal exercida pela pista sobre o carro durante o percurso de até . Ignore as resistências do ar e de rolamento.
Passo 1
Vamos lá a mais uma questão! Esta questão é a continuação da questão 41. Temos que obter as forças normais máximas e mínimas para a mesma geometria do problema anterior.
O interessante é que esta questão pode ser resolvida bem fácil se nós soubermos os pontos que temos que calcular as forças normais. Agora, se a gente não souber, vamos ter que calcular para todos os trechos!!!
Então, vamos utilizar os nossos conhecimentos para entender o que está se passando por aqui!
Passo 2
Vamos analisar inicialmente a trajetória circular no trecho . O nosso diagrama de corpo livre foi:
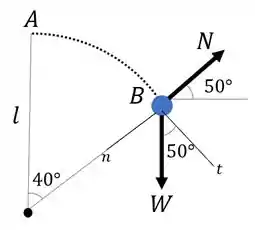
Como existe uma força centrípeta, nós obtivemos que:
Portanto, quanto maior a velocidade, menor a força normal. Logo, a força normal aqui será mínima em , sendo .
Passo 3
Agora vamos para o trecho . Aqui é uma trajetória retilínea. Logo, não há aceleração centrípeta na direção normal da curva. Fazendo o diagrama de corpo livre, temos:
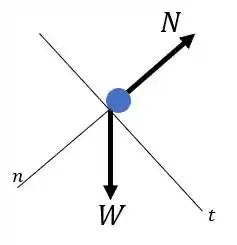
Então, fazendo o somatório de forças na direção normal, temos:
Logo, a força normal neste trecho é maior do que no trecho .
Passo 4
Agora, vamos analisar no trecho . Novamente, fazendo o diagrama de corpo livre, temos:
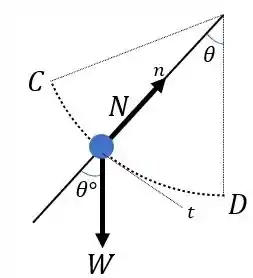
Lembrando, como aqui temos um trecho circular, teremos a presença de uma aceleração centrípeta (assim como foi no Passo 2). Então, fazendo o somatório de forças na direção normal, teremos:
Então, a força será máxima quando for máximo . Logo, será máxima no ponto . E consequentemente, será mínima em . Agora, precisaremos calcular elas para saber se serão a maior e menor em todo o trecho.
Passo 5
Vamos começar analisando no ponto . De cara podemos esperar que a força normal aqui será ainda maior do que a força normal em . Isto deve ocorrer pois a força normal está na direção normal a curva (haverá força centrípeta).
Portanto, como o carrinho possui maior velocidade, então, a força normal deverá ser elevada (fica a dica para a força normal máxima!!!). Desta forma, concluímos aqui que esta força será maior do que no ponto .
Agora podemos partir para o cálculo do ponto . Precisaremos então da velocidade do carrinho neste ponto. Calculando o trabalho da força peso e as energias cinéticas associadas, temos:
Portanto, pelo princípio de trabalho e energia, temos:
E assim chegamos à força normal de:
Passo 6
Para finalizarmos a questão, basta verificarmos qual foi a maior e qual a menor força normal obtida. Assim, chegamos aos seguintes valores: