Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 121

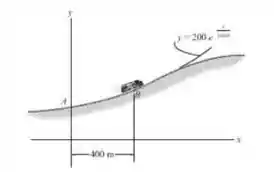
Um trem passa pelo ponto B com uma velocidade escalar de 20   m / s , a qual está diminuindo em a t = - 0,5   m / s 2 . Determine a intensidade da aceleração do trem neste ponto.

Passo 1

Precisamos determinar a intensidade da aceleração. Como já nos foi dado a sua componente tangencial, só precisamos calcular a sua componente normal. Mas aí a gente se questiona: e cadê o raio de curvatura? Este é o ponto mais difícil da questão. Para calcularmos o raio de curvatura, será necessário utilizarmos a seguinte equação:

ρ = 1 + d y d x 2 3 / 2 d 2 y d x 2

Como sabemos que o valor de x = 500 , basta fazer as derivações e aplicar este valor na função! Depois, basta calcular a aceleração normal e obter o valor da aceleração no ponto B.

Passo 2

Vamos determinar qual o raio de curvatura. Para isto, utilizaremos a fórmula do Passo 1. Primeiramente, derivaremos a função que governa a nossa curva duas vezes. Sendo assim:

y = 200 e x 1000

y ' = d y d x = e x 1000 5

y ' ' = d 2 y d x 2 = e x 1000 5000

Substituindo na fórmula do raio de curvatura, temos:

ρ = 1 + e 2 x 1000 25 3 / 2 e x 1000 5000

Quando x = 400 , temos:

ρ = 3809   m

Passo 3

Agora, calculando a componente normal, temos:

a n = v 2 ρ = 20 2 3809 = 0,105   m / s 2

Portanto, a intensidade da aceleração é:

a = a t 2 + a n 2

a = - 0,5 2 + 0,105 2

a = 0,51   m / s 2

Resposta

a = 0,51   m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula se desloca ao longo da trajetória curva mostrada. A partícula tem uma velocidade v A = 4m / s no instante t A e uma velocidade v B = 4,2m / s no instante t B . Determine os valores médio
Um carro de teste parte do repouso em uma pista horizontal circular de 80m de raio e aumenta sua velocidade a uma taxa uniforme para atingir os 100k m / h em 10 segundos. Determine o módulo a da acele
O carro passa por uma depressão na estrada em A com uma velocidade constante que dá ao seu centro de massa G uma aceleração igual a 0,5 g . Se o raio de curvatura da estrada em A é de 100m , e se a di
O carro se desloca sobre uma superfície horizontal sem qualquer deslizamento de seus pneus. Para cada um dos oito vetores de aceleração horizontal, descreva em palavras o movimento instantâneo do carr
O carro viaja com uma velocidade constante da parte inferior A da depressão para o topo B da elevação. Se o raio de curvatura da estrada em A é ρ A = 120m e a aceleração do carro em A é 0 , 4 g , dete