Um automóvel tem velocidade escalar de 24m / s no ponto A e tem aceleração a , tendo intensidade de 3m / s 2 , atuando na direção mostrada. Determine o raio de curvatura da trajetória no ponto A e a componente tangencial da aceleração.

a t = 3 3 2 ≅ 2,6m / s 2 ρ = 384m

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 12.Problemas - Ex. 116

Um automóvel tem velocidade escalar de no ponto A e tem aceleração , tendo intensidade de , atuando na direção mostrada. Determine o raio de curvatura da

trajetória no ponto A e a componente tangencial da aceleração.

Passo 1

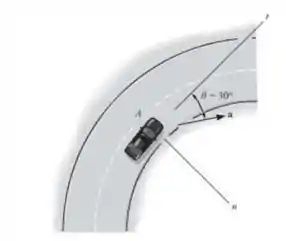
Para resolvermos esta questão, é de fundamental utilizarmos a imagem dada e relações trigonométricas! Vamos decompor o vetor aceleração na sua direção tangencial e normal. Portanto,

Agora fica tudo fácil. Para calcularmos a aceleração tangencial basta fazermos uma substituição direta. Já para encontrarmos o raio de curvatura, basta relacionar com a equação da componente normal da aceleração (muito fácil também né!)

Passo 2

Vamos calcular inicialmente a componente tangencial da aceleração. Como a intensidade da aceleração é dada por , temos:

Passo 3

Para calcularmos o raio de curvatura, vamos determinar inicialmente qual o valor da componente normal . Portanto,

Agora, basta substituir este valor na seguinte relação:

Como a velocidade é , temos:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma partícula P se desloca na trajetória circular mostrada. Desenhe o vetor aceleração a e determine o seu módulo a para os seguintes casos:(a) a velocidade v é 1,2m / s e é constante,(b) a velocidade

2/165) Para as condições do Prob. 2/164 , determine θ ' como uma função do tempo .

O foguete lançado verticalmente e o radar de rastreamento do Prob. 2/147 são apresentados aqui novamente. No instante em que θ = 60 ° , as medidas fornecem θ ˙ = 0,03r a d / s e r = 7500m , e a aceler

O deslocamento angular da centrífuga é dado por θ = 4 t + 30 e - 0,03 t - 30r a d , onde t é expresso em segundos e t = 0 é o instante da partida. Se o ser humano perde a consciência em um nível de ac

2/168) Uma cápsula P de fogos de artifício lançada em uma trajetóra vertical tem uma aceleração y dada por a y = - g - k v 2 , onde o último termo é devido ao arrasto aerodinâmico . Se a velocidade da