Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 34
Determine a aceleração máxima que pode ser alcançada pelo carro de 775 kg sem que as rodas dianteiras A deixem a pista ou as rodas motrizes traseiras B deslizem na pista. O coeficiente de atrito estático é . O centro de massa do carro está em G e as rodas dianteiras estão livres para rodar. Despreze a massa de todas as rodas.
Passo 1
Devemos notar que o enunciado menciona a força nos pares de rodas, então trataremos o carro como se tivéssemos somente um ponto de apoio em A e outro em B conforme o esquema a seguir:
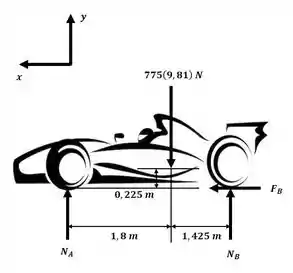
Para a resolução desse exercício, iremos adotar a aceleração da gravidade local g = 9,81 m/s².
Como ponto de partida, escreveremos todas as equações de movimento do sistema:
Passo 2
Para resolver esse exercício, podemos seguir dois caminhos, assumir que as rodas dianteiras estão na iminência de deixar a pista, ou seja, , ou assumir que as rodas traseiras estão na iminência de derrapar, fazendo e então ver qual das duas condições atende ao que é pedido.
Primeiramente, vamos assumir a hipótese de , sendo assim, subsituindo esse valor nas equações do passo 1:
E substituindo esse valor em:
Por fim, para obter o valor teórico de , utilizamos a última equação obtida no passo 1:
No entanto, sabemos que o valor máximo de para que as rodas traseiras não deslizem é dado por:
Logo, podemos observar que , o que faria com que as rodas traseiras deslizassem.
Passo 3
Sendo assim, partiremos para nossa segunda hipótese:
Resolvendo as equações de movimento do passo 1 com essa condição, temos:
Substituindo esse valor na segunda equação do passo 1, obtemos o valor de :
Sendo assim:
E, substituindo esse valor na primeira equação do passo 3:
E, finalmente, encontraremos a máxima aceleração do centro de massa substituindo o valor de na primeira equação do passo 1: