Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 64
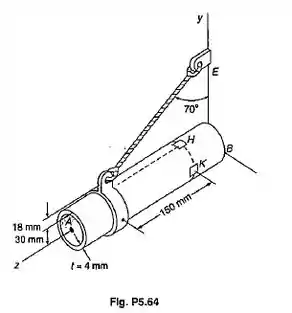
O tubo padrão AB tem um diâmetro externo de 60 mm e uma espessura da parede de 4 mm. Sabendo-se que a tensão no cabo DE é de 18 kN, determinar as tensões normal e de cisalhamento no (a) ponto H; (b) ponto K.
Passo 1
Do enunciado temos
Com isso podemos calcular A, J e I.
Passo 2
Vamos agora decompor a força F de 18 kN em seus respectivos eixos
Passo 3
Fazendo agora uma análise das forças teremos
Passo 4
Com essas informações spodemos comçar a calcular as tensões normal e de cisalhamento no ponto H
Observa que esse valor é zero já que não temos torque no eixo z
Resposta
Exercícios de Livros Relacionados
Faça uma representação gráfica da distribuição da tensão de cisalhamento na seção transversal de uma haste com raio c. Quantas vezes a tensão de cisalhamento máxima é maior que a tensão de cisalhament
A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a tensão de cisalhamento máxima desenvolvida nas juntas coladas. Os
Determine a tensão de cisalhamento nos pontos B e C localizados na alma da viga de fibra de vidro.
Determine a tensão de cisalhamento máxima que age na seção crítica da viga de fibra de vidro.
A viga é composta por três tábuas coladas nas linhas de junção A e B. Se for submetida ao carregamento mostrado na figura, determine a força de cisalhamento vertical máxima à qual resiste a aba superi