Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 144
Um único extensômetro de deformação é colado a um eixo de transmissão maciço de aço, com de diâmetro e formando um ângulo de 25° com uma linha paralela ao eixo da peça. Sabendo-se que , determinar o torque indicado, se a leitura do extensômetro acusa .
Passo 1
Fala aí, galerinha sapeca! Para resolver essa questão a gente precisa observar que existem apenas tensões cisalhantes (devido ao torque) e as tensões normais são nulas. Dessa forma vamos ter:
E a tensão cisalhante vai ser dada pela equação que a associa ao torque:
É com essa equação que a gente vai achar o torque pedido na questão. Então partiu!
Passo 2
Se a gente quer achar o torque então a gente tem que achar todos os outros termos antes, a distância, que é igual ao raio; o momento polar de inércia e a tensão cisalhante . Vamos começar:
O momento de inércia de um cilindro é dado por:
A tensão de cisalhamento vamos deixar para o próximo passo.
Passo 3
Para achar a tensão de cisalhamento a gente precisa lembrar que a deformação angular vai ser igual à tensão de cisalhamento sobre a resistência à torção , assim:
Mas temos uma questão aqui, o extensômetro foi colocado a um ângulo de 25°, isso faz com que o resultado não seja tão direto assim. A gente tem que fazer um esqueminho do ciclo de Mohr:
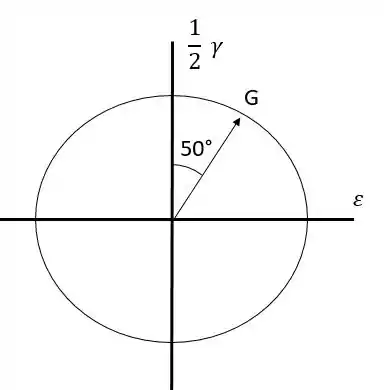
Show, mas de onde surgiu esse ângulo de 50°? Surgiu porque o ângulo dentro do c´rculo de Mohr é o dobro do “real”.
Então quando vai valer a deformação do ponto onde estamos analisando? Para saber isso a gente tem que pegar a projeção horizontal e portanto vai valer:
Mas essa deformação é exatamente a fornecida no problema e vale , logo a gente vai poder achar :
Agora é só substituir em
Passo 4
Com isso podemos achar a torção: