Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 46
A barra uniforme de é liberada a partir do repouso na posição horizontal mostrada e atinge o canto fixo no centro de percussão da barra. Determine a componente da força exercida pelo mancal sobre a barra pouco antes do impacto, durante o impacto, e logo após o impacto.
Passo 1
Existe uma forma muito simples de resolver esse problema, e envolve o uso do centro de percussão da barra que gira em torno do eixo fixo em .
O primeiro passo é encontrar esse centro de percussão:
Onde é o raio de giração em relação ao eixo fixo em . Ele pode ser calculado da seguinte forma:
Onde é o momento de inércia em relação a esse mesmo eixo, para encontrar uma expressão para isso, vamos usar o teorema dos eixos paralelos:
E é a distância entre o centro de massa da barra e o ponto :
Agora já podemos calcular :
E é a distância entre o centro de massa e o ponto , então:
Passo 2
Beleza, então o centro de percussão é um ponto sobre a barra, a uma distância do ponto .
A propriedade útil desse ponto é que a soma dos momentos em relação a ele é zero em todos os instantes que foram mencionados no enunciado:
E então podemos escolher qualquer instante para aplicar essa equação, e encontraremos resultados válidos para todo o movimento.
Se tomarmos o instante logo antes do impacto:
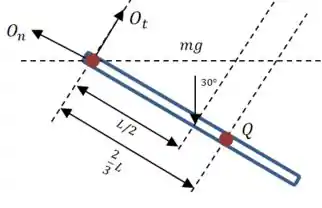
E esse é o valor de em todos os instantes mencionados no enunciado.
Resposta
A componente tangencial da força exercida pelo mancal é de em todos os instantes mencionados.