A barra semicircular uniforme de massa e raio é livremente articulada em torno de um eixo horizontal através de . Se a barra é liberada a partir do repouso na posição mostrada, onde é horizontal, determine a aceleração angular inicial da barra e a expressão para a força exercida sobre a barra pelo pino em . (Observe atentamente que a aceleração tangeencial inicial do centro de massa não é vertical).

Agora queremos calcular a força exercida sobre a barra pelo pino em . É uma boa ideia dividir essa força em duas componentes, uma normal e uma tangencial:

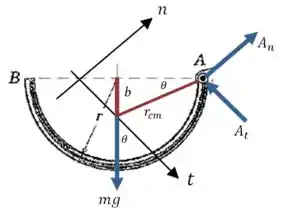
Onde e são distâncias que podemos calcular depois. Vamos aplicar a segunda lei de Newton nas duas direções, sempre pensando no centro de massa do sistema.

Na direção normal a aceleração do centro de massa é nula, então:

E as forças que atuam nessa direção são , e uma componente do peso:

Na direção tantencial, a aceleração do centro de massa pode ser calculada a partir da aceleração angular e da distância até o ponto :

E as forças que atuam nessa direção são e a outra componente da força peso:

Agora vamos encontrar expressões para , e , para então substituí-las nas expressões de e .

Podemos consultar uma tabela para encontrar , que é a posição do centro de massa em relação ao eixo do desenho:

E ainda pelo desenho, podemos usar o teorema de pitágoras para calcular :

E por fim, podemos calcular através do seu seno e cosseno:

Agora vamos substituir tudo e encontrar a expressão para :

Então:

E agora substituímos a expressão para no primeiro termo da raiz, de forma que a fração fica igual a , e então:

E finalmente: