Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 53
Usando o método do trabalho virtual, determine a reação em E.
Passo 1
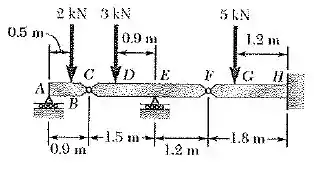
Primeiro vamos entender o problema! Temos forças verticais para baixo e por conta dessas forças e se não tivéssemos o suporte E teríamos um deslocamento no ponto E de , no ponto B de e assim por diante.
Certo, então vamos tirar algumas relações por semelhança de triângulo, observe a partir do ponto H, temos:
Outra:
Outra:
Passo 2
Agora que já achamos a relação dos deslocamentos, só basta utilizar o trabalho virtual que teremos nossa solução. De modo que o trabalho virtual é dado por:
E como,
Então,
Passo 3
Já achamos a relação agora é só substituir com as relações que encontramos no Passo 1, então:
Simplificando, teremos:
Portanto,
Resposta
Exercícios de Livros Relacionados
Quando as forças são aplicadas às alças do saca-rolhas, determine a força puxada desenvolvida na rolha.
A prensa perfuradora consiste em um cilindro R , barra de conexão A B e um volante. Se um torque de M = 50 N ⋅ m for aplicado ao volante, determine a força F aplicada no cilindro para manter a barra n
Determine a intensidade do momento de binário M necessário para suportar o cilindro de 20 k g na configuração mostrada. A ranhura lisa em B pode deslizar livremente dentro da ranhura. Despreze a massa
A barra uniforme A B tem um peso de 50 N . Se a mola D C está livre quando θ = 0 ° , determine o ângulo θ para o equilíbrio usando o princípio do trabalho virtual. A mola sempre permanece na posição h
As ligações uniformes A B e B C pesam cada uma 10 N e o cilindro pesa 100 N . Determine a força horizontal P necessária para manter o mecanismo em θ = 45 ° . A mola tem um comprimento livre de 150 m m