Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 8.2 - Ex. 11

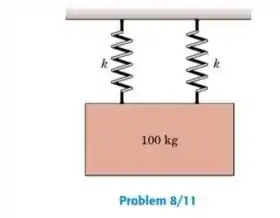
Se a massa de 100 kg tem uma velocidade para baixo de 0.5 m/s quando cruza a sua posição de equilibro, calcule o módulo a m a x de sua aceleração máxima. Cada uma das duas molas possui uma rigidez k = 180 k N / m .

Passo 1

A massa tem velocidade inicial dada pelo enunciado exatamente ao passar pela posição de equilíbrio, o que significa que a posição inicial é zero, portanto a equação do movimento oscilatório será:

x = x 0 ˙ ω n s e n ω n t

Passo 2

Para escrevermos a aceleração máxima, vamos primeiro precisar calcular a frequência natural de vibração, como as duas cordas estão em paralelo, as constantes de mola podem ser somadas. A equação da frequência então ficará:

ω n = 2 k m

E substituindo os valores:

ω n = 2 ( 180000   N / m ) 100 k g = 60   r a d / s

Passo 3

Fazendo a derivada de x:

x ˙ = x 0 ˙ c o s ω n t

E derivando novamente para encontrarmos a equação da aceleração:

x ¨ = - ω n x 0 ˙ s e n ω n t

Substituindo cada valor das grandezas:

x ¨ = - 60 r a d / s 0.5 m / s   s e n 60 r a d / s t

Como a função seno deve ser máximo para que o módulo da aceleração aceleração seja máximo:

x ¨ m a x = 60 r a d / s 0.5 m / s = 30 m / s 2

Resposta

x ¨ m a x = 60 r a d / s 0.5 m / s = 30 m / s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

141. Na figura são apresentados os elementos de um medidor de deslocamentos usado para estudar o movimento y b = b ⋅ s e n ( ω t ) da base. O movimento da massa em relação à carcaça é registrado no ci
137. Uma máquina de 200k g se apoia sobre quatro suportes no chão, cada um dos quais possui uma constante de mola efetiva k = 250k N / m e um coeficiente de amortecimento viscoso efetivo c = 1000 N ⋅
143. Determine e represente graficamente a resposta x = f ( t ) para o oscilador linear não amortecido, submetido à força F que varia linearmente com o tempo, durante os primeiros 3 / 4 de segundo, co
139. A massa de um sistema criticamente amortecido, que possui uma frequência natural ω n = 4r a d / s , é liberada a partir do repouso com um deslocamento inicial x 0 . Determine o tempo t necessário
144. O oscilador linear amortecido de massa m = 4k g , constante de mola k = 200N / m , e o fator de amortecimento viscoso ζ = 0,1 está inicialmente e, repouso em uma posição neutra, quando é submetid