Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 116

Para a viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão no ponto B .

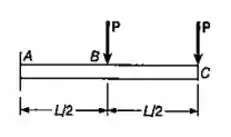
Passo 1

Fala aí galera, vamos pra mais um exercício de Resmat. Neste exercício temos uma viga com uma extremidade engastada e outra livre. Com isso, por superposição tem-se que:

Para o primeiro carregamento:

y 1 = P 6 E I ( x 3 - 3 L x 2 ) y 1 = P 6 E I L 2 3 - 3 L L 2 2 y 1 = - P L 3 48 E I

Para o segundo caso:

y 2 = P 6 E I ( x 3 - 3 L x 2 ) y 2 = P 6 E I ( L 3 - 3 L L 2 y 2 = P L 3 8 E I

Com isso, temos que nossa deflexão na extremidade é dada por:

y C = y 1 + y 2 y C = - P L 3 48 E I + P L 3 8 E I y C = - 7 P L 3 48 E I

Passo 2

Em seguida, para encontrarmos a declividade na extremidade, temos que utilizar as relações de apoios fornecidas no apêndice D do livro. Temos :

θ = θ 1 + θ 2

A força P que atua no ponto B não gera declividade nele e, portanto:

θ = - P L 2 2 E I + 0 θ = - P L 2 2 E I θ = - P L 2 2 E I

Resposta

y C = - 7 P L 3 48 E I

θ = - P L 2 2 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a reação no apoio móvel e desenhe o diagrama de momento fletor para a viga e o carregamento mostrados nas figuras.
Para a viga e o carregamento mostrados, determine a reação no apoio móvel quando w 0 = 15k N / m .
Para a viga e o carregamento mostrados nas figuras, determine a reação no apoio móvel.
Para a viga e o carregamento mostrados, determine (a) a equação da linha elástica e (b) a deflexão na extremidade livre.
Para a viga e o carregamento mostrados na figura, determine a deflexão no ponto C . Use E = 200G P a .