Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 8.Problemas - Ex. 70

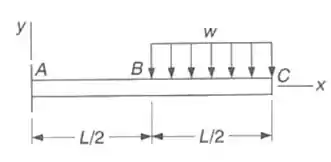
Para a viga com o carregamento mostrado, determinar a) a equação da linha elástica b) a deflexão na extremidade livre.

Passo 1

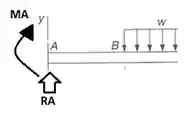
E ai gurizada tudo belezinha??? Vamos analisar a viga em questão... antes de tudo vamos desenhar o diagrama de corpo livre :D

Primeiramente vamos calcular o somatório de forças em Y.

+ ↑ ∑ F y =   0

R a - 1 2 w L = 0  

R a = w L / 2

Calculando o somatório do momento em A temos:

+ ↺ ∑ M a =   0

- M a - ( w L 2 ) × 3 L / 4 =   0

M a = - 3 w L 2 8

Considerando o trecho da viga variando de 0

+ ↺ ∑ M =   F   x   d

M = - 3 w L 2 8 + w L x 2

Considerando o trecho da viga variando de L/2

+ ↺ ∑ M x = 0

3 w L 2 8 - w L x 2 + w 2 × x - L 2 2 + M = 0

M = - 3 w L 2 8 + w L x 2 - w 2 × x - L 2 2

Passo 2

Agora vamos achar a equação linear, vem comigo :D

E I d 2 y d x 2 = M = - 3 w L 2 8 + w L x 2 - w 2 × x - L 2 2

Integrando a equação acima temos....

E I d y d x = - 3 w L 2 x 8 + w L x 2 4 - w 6 × x - L 2 3 + C 1

Integrando novamente teremos...

E I y = - 3 w L 2 x 2 16 + w L x 3 12 - w 24 × x - L 2 4 + C 1 x + C 2

y = w E I - 3 L 2 x 2 16 + L x 3 12 - 1 24 × x - L 2 4

Derivando a equação acima temos...

d y d x = w E I - 3 L 2 x 8 + L x ² 4 - 1 6 × x - L 2 3

Passo 3

Agora para encontrarmos a deflexão vamos considerar que: x= L

Y c = w L 4 E I × ( - 3 16 + 1 12 - 1 24 1 2 4 = - 41 384 w L 4 E I

 

Resposta

a )   w E I - 3 L 2 x 8 + L x ² 4 - 1 6 × x - L 2 3

b )   Y c = - 41 384 w L 4 E I

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma viga em balanço com o carregamento mostrado, determinar a declividade e a deflexão no ponto B. Usar E = 200 G P a .Deflexão do ponto B
Para a viga com o carregamento mostrado, determinar:A reação em A
As cargas distribuídas mostradas são suportadas por pequenas vigas, que descansam sobre a viga em balanço AB. Usando E = 200G P a , determinar a declividade e a deflexão no ponto B da viga em balanço.
As cargas distribuídas mostradas são suportadas por pequenas vigas, que descansam sobre a viga em balanço AB. Usando E = 200G P a , determinar a declividade e a deflexão no ponto B da viga em balanço.
Para a viga com o carregamento mostrado, determinar:A reação em D