Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 5.Problemas - Ex. 130

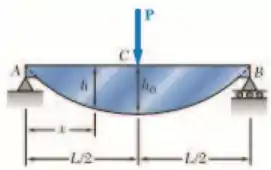
A viga AB, que consiste em uma placa de alumínio de espessura uniforme b e comprimento L, e deve suportar a força w mostrada. (a) Sabendo que a viga deve ser de resistência constante, expressa h em termos de x, L, e h0.para a parte AC da viga (b) Determine a força máxima admissível se L =800mm, h0= 200 mm, b = 25 mm 0 mm, 0 w = 300 kN / m e σ= 72 MPa.

Passo 1

Fala aí gurizada tudo belezinha?? O exercício pede que a gente determine ue a viga deve ser de resistência constante, expressa h em termos de x, L, e h0.para a parte AC da viga, então vem comigo :D. Primeiramente vamos determinar o momento em C para acharmos a reação em A.

R a = R b = P 2

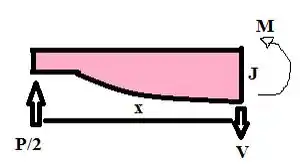
Fazendo o somatório do momento em J temos:

M = F x d =   - P 2 x + M = 0

M = P x 2

Temos que:

S = M σ = P x 2 σ

Para uma seção retangular temos: S = 1 6 b h ²

Igualando temos:

1 6 b h 2 = = P x 2 σ

Isolando h temos:

h = h o 3 P L 2 σ b = 2 x L

Passo 2

Agora gurizada podemos determinar o valor de P substituindo na equação que encontramos no passo 1 :D

h = h o 3 P L 2 σ b

Isolando P temos:

P = 2 σ b h 2 3 L = 2 x 72 x 10 6 x 0,025 x 0,2 2 3 x 0,8 = 60   x 10 3 N = 60 K N

Resposta

  1. h = h 0 2 x L
  2. 60   K N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra e o carregamento da aplicação de conceito 4.1, determine:P raio de curvatura ρ ; O raio de curvatura ρ ' num plano transversal;O ângulo entre os lados originalmente verticais da barra. Us
No P r o b .4.28 , determine:O valor de h para o qual a tensão máxima σ m é a menor possível e.O valor correspondente de k.
Uma viga de aço laminado W 200 x 31,3 está submetido a um momento M de 45k N m . Sabendo-se que E = 200G P a e ϑ = 0 , 29 , determine:O raio de curvatura ρ e ;O raio de curvatura ρ ' da seção transver
A viga retangular mostrada na figura é feita de um plástico para o qual o modulo de elasticidade em tração é metade de seu valor em compressão. Para um momento fletor M = 600N m , determine.A tensão d
Uma barra retangular é feita de um material para o qual o modulo de elasticidade é E t em tração e E c em compressão. Mostre que a curvatura da barra em flexão pura é 1 ρ = M E r I Em que: E r = 4 E t