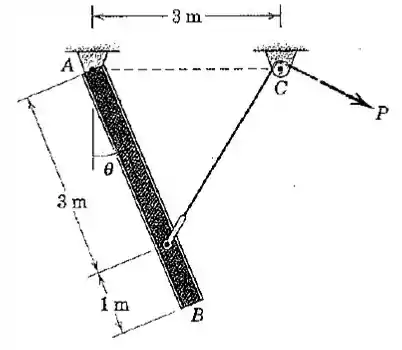
A viga uniforme AB de 100kg está perdurada inicialmente em repouso θ=00 quando a força constante P=300 N é aplicada ao cabo. Determine (a) a velocidade angular máxima atingida pela viga com o ângulo θ correspondente e (b) o ângulo máximo θmáx alcançado pela viga.
Passo 1
Definir a equação de momento:
Passo 2
Resolver equação considerando α = 0; resolvendo para θ teremos:
e
Passo 3
Agora considerando ω = 0 teremos:
Resposta
Assim θ = 22,4 ; ω=0,680 rad/s e θmax = 45,9°: