Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 7ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 7º - Capítulo 3.Problemas - Ex. 96
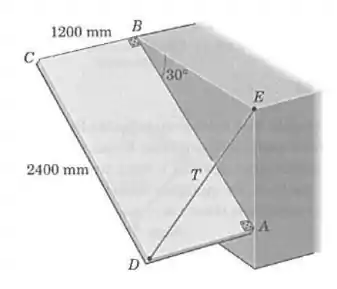
O painel retangular uniforme tem uma massa de e tem dobradiças entre seus vértices e e a superfície vertical rígida. Um arame ligando a mantém horizontais as bordas e . A dobradiça pode sustentar esforços ao longo do eixo , enquanto a dobradiça suporta apenas força normal ao eixo . Ache a força trativa no arame e o módulo da força suportada pela dobradiça .
Passo 1
Vamos começar escrevendo a força que age sobre o arame em forma vetorial:
Isso vai ser muito útil para facilitar o cálculo dos momentos. Vamos desenhar as forças envolvidas e definir alguns eixos:
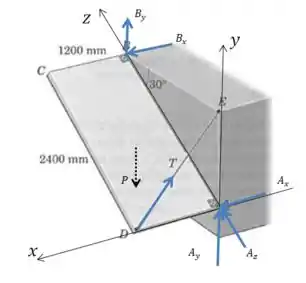
Passo 2
Agora vamos analisar o equilíbrio dos momentos em relação a cada eixo. Começando pelo eixo . Nesse caso todas as componentes nessa direção terão momento nulo, e as componentes que cruzam esse eixo também, então:
E então:
Passo 3
E agora vamos ver o momento em relação ao eixo . Nesse caso tanto a tração quanto as forças em terão momento nulo, e o mesmo acontece para a componente e (já que essas duas são paralelas ao eixo).
Passo 4
E por último, o momento em relação ao eixo . Nesse caso ficamos apenas com a componente do peso e da tração, além da componente . As outras forças têm linhas de ação que cruzam o eixo, ou são paralelas a ele.
E então o módulo da força é:
Resposta
As forças são e .