Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 17.Problemas - Ex. 85

O volante de 50 kg tem um raio de giração em relação a seu centro de massa k O = 250   m m . Ele gira com uma velocidade angular constante de 1200 rev/min antes de o freio ser aplicado. Se o coeficiente de atrito cinético entre a sapata do freio B e a borda da roda μ k = 0,5 , determine a força constante P que tem de ser aplicada à alavanca do mecanismo de frenagem a fim de parar a roda em 100 revoluções.

Passo 1

Iremos considerar a aceleração da gravidade g = 9,81   m / s 2 .

Começaremos o exercício convertendo a velocidade angular inicial para radianos por segundo:

ω 0 = 1200 r e v m i n 2 π   r a d 1   r e v 1   m i n 60   s → ω 0 = 40 π   r a d / s

E também o número de revoluções para radianos:

θ = 100 r e v 2 π   r a d 1   r e v → θ = 200 π   r a d

Agora podemos Torricelli para o movimento angular:

↺ +   ω 2 = ω 0 2 + α θ - θ 0

0 2 = 40 π 2 + 2 α 200 π - 0 → α = - 12,57   r a d / s 2

Passo 2

Agora iremos aplicar o somatório de momento em torno do ponto A usando o diagrama a seguir:

↺ +   ∑ M A = 0

N B 1 + 0,5 N B 0,2 - P 1,5 = 0

N B = 1,3636   P

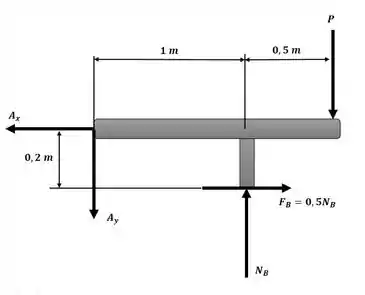
Passo 3

Antes de aplicarmos o somatório de momentos em torno do ponto O, iremos calcular o momento de inércia do volante com relação ao seu centro de massa:

I O = m k O 2 = 50 0,25 2 → I O = 3,125   k g . m 2

Sendo assim, com o auxílio da imagem a seguir, temos:

↺ + ∑ M O = I O α

0,5 N B 0,3 = 3,125 ( 12,57 )

Substituindo a expressão de N B obtida no passo 2:

0,5 1,3636   P 0,3 = 3,125 ( 12,57 )

P = 192   N

Resposta

P = 192   N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O avião a jato tem uma massa de 22Mg e um centro de massa em G. Se um cabo de rebocar está fixado à parte superior do trem de pouso do nariz e exerce uma força T = 400N , como mostrado, determine a ac
A empilhadeira manual tem uma massa de 70 kg e centro de massa em G. Se ela levanta a bobina de 120 kg com uma aceleração de 3 m/s², determine as reações em cada uma das quatro rodas. A carga é simétr
O dragster tem uma massa de 1500 kg e um centro de massa em G. Se o coeficiente de atrito cinético entre as rodas traseiras e o pavimento é μ k = 0,6 , determine se é possível para o motorista levanta
Uma biela é sustentada por um fio de faca no Ponto A; o período de suas pequenas oscilações é observado como 0,87 s. A haste é então invertida e suportada por um fio de faca no Ponto B e o período de
O compressor mostrado tem uma massa de 250 kg e opera a 2.000 rpm. Nesta condição de operação, vibração indesejável ocorre quando o compressor é acoplado diretamente ao solo. Para reduzir a vibração d