Tubos de Paredes Finas
Teoria
Introdução
Normalmente, usamos eixos cilíndricos para a transmissão de torques.
Então normalmente, a gente só se preocupa em calcular a tensão de cisalhamento e o ângulo de torção em eixos.
Mas às vezes, usamos um tubo de paredes finas no lugar de um eixo cilíndrico.
Um exemplo é o tubo abaixo, retangular, de dimensões externas , com uma espessura nas faces superior e inferior e uma espessura nas faces laterais:
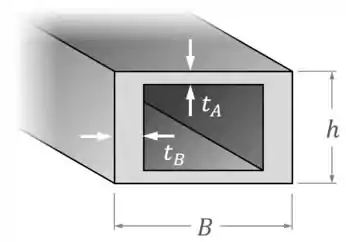
Para tubos como esse, as fórmulas e não servem mais.
Então nesse tópico, vamos ver quais são as fórmulas que servem para esses tubos.
Tensão de Cisalhamento Média
A primeira coisa que precisamos saber sobre esses tubos é que não é fácil calcular as tensões de cisalhamento máximas neles.
Então ao invés disso, calculamos as tensões de cisalhamento médias usando a fórmula:
Onde:
- é o torque interno no tubo;
- é a espessura da região do tubo onde está sendo calculada a tensão de cisalhamento média ;
- & é a área média do tubo, que vamos aprender a calcular a seguir.
Então dessa forma, caso o nosso tubo tivesse uma espessura constante, a tensão cisalhante média nele todo seria .
Como no nosso exemplo, o tubo tem duas espessuras diferentes, ele vai ter:
- Uma tensão cisalhante média em todos os pontos em que o tubo tiver a espessura ;
- E uma tensão cisalhante média em todos os pontos em que o tubo tiver a espessura .
Área Média
E essa tal “área média do tubo” ? O que é isso?
Ela é a média entre a área delimitada pelas linhas externas da seção do tubo e a área delimitada pelas linhas internas, como mostra a imagem abaixo:
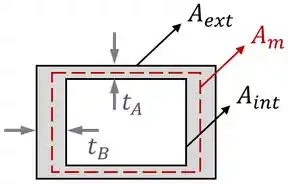
Dimensões Médias e o Cálculo da Área Média
Normalmente, para calcular , nós buscamos definir as dimensões médias do tubo.
Para tanto, podemos observar como a distância entre uma dimensão externa e uma dimensão média do tubo é igual à metade da espessura daquela região:
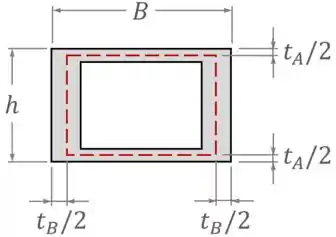
Com isso, conseguimos definir, para o nosso exemplo, as dimensões médias e , resultando em uma área média , como mostra a figura abaixo:
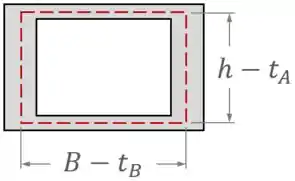
Ângulo de Torção
Já para calcular o ângulo de torção em um tubo de paredes finas, nós usamos a fórmula:
De início, essa fórmula parece complicada, mas se a gente olhar para ela com calma, vamos ver que ela não é tão difícil assim.
Primeiro, temos que:
- é o torque interno no tubo;
- é o comprimento;
- é a área média;
- & é a espessura.
Além disso, de novo, nós temos:
- O módulo de elasticidade transversal do material do tubo, normalmente dado em ;
- E o perímetro da área média , que está nessa equação como a variável de integração da integral .
Então para sabermos calcular o ângulo de torção em um tubo de paredes finas, só nos resta saber como calcular essa integral:
Cálculo da Integral
A primeira coisa que nós podemos observar sobre essa integral é o símbolo dela:
Essa bolinha na integral significa que ela é uma integral fechada ou de contorno.
Isso quer dizer que essa integral dá uma volta completa por sua variável de integração, que, nesse caso, é o perímetro da área média.
Então para calcular essa integral, você pode:
- Dividir o perímetro da área média em pequenos trechos , , e ;
- E imaginar a integral dando uma volta por esses trechos,
Como na imagem abaixo:
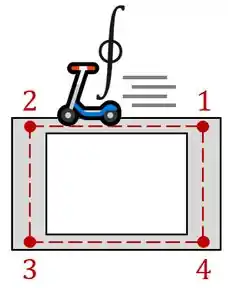
Fazendo isso, nós vamos estar abrindo a nossa integral fechada em uma sequência de integrais abertas:
Em seguida, como cada trecho tem uma espessura constante – igual à para os trechos e e para e – podemos tirar essas espessuras das integrais:
Com isso, as integrais que sobram vão ser iguais ao perímetro de cada trecho, de tal forma que:
Então sempre que você precisar calcular essa integral , basta aplicar essa metodologia da volta. 🛴😎
Finalização
Nessa matéria de tubos de paredes finas, a teoria é basicamente as fórmulas e e o cálculo da área média .
O que importa mais é ter um pouco de prática para ter a confiança de lidar com qualquer formato de tubo que seus professores inventarem.
Então se você quiser treinar um pouco disso, é só seguir para os exercícios. 👊
Tensão de Cisalhamento Média
Área Média
Ângulo de Torção
Finalização
Exercícios Resolvidos
Exercício Resolvido #1
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 163-5.98.
O tubo de aço inoxidável 304 tem espessura de . Se a tensão de cisalhamento admissível for , determine o torque máximo que ele pode transmitir. Calcule também o ângulo de torção de uma extremidade do tubo em relação à outra se o tubo tiver de comprimento. Despreze as concentrações de tensão nos cantos. As dimensões médias são mostradas na figura.
Dados: .
Passo 1
O que está acontecendo?
O tubo de paredes finas retangular tem dimensões médias de e . Consequentemente, ele tem uma área média e um perímetro da área média :
Além disso, ele possui:
- Uma espessura constante ;
- Uma tensão de cisalhamento admissível ;
- Um módulo de elasticidade transversal ;
- & um comprimento .
Devido a um torque aplicado, ele vai sofrer uma tensão de cisalhamento média e um ângulo de torção que vão ser dados pelas fórmulas:
E o que é que o exercício quer?
Primeiro, ele quer saber qual é o torque máximo que pode ser aplicado de tal forma que a tensão de cisalhamento média na peça não ultrapasse a admissível:
Em seguida, ele quer que a gente use o valor encontrado para para calcular o ângulo de torção no tubo correspondente.
Passo 2
Então para encontrar o torque máximo, vamos pegar a nossa condição de projeto:
E desenvolvê-la, até que seja possível isolar o torque .
A primeira coisa que podemos fazer é aplicar a fórmula da tensão de cisalhamento média para tubos de paredes finas:
Fazendo isso, a nossa condição de projeto fica assim:
Isolando o torque , temos que:
Finalmente, substituindo os valores:
- ;
- ;
- & ,
Encontramos que:
Reescrevendo isso em , temos que:
Ou seja, é o torque máximo que pode ser transmitido por esse tubo.
Passo 3
Agora, para a segunda parte do exercício, vamos calcular o ângulo de torção nesse tubo de paredes finas aplicando a sua fórmula:
No caso do nosso tubo, a espessura é constante: ela é sempre igual à ao longo de todo o perímetro .
Então podemos colocar a espessura do lado de fora da integral:
Em seguida, temos que a integral de todos os pedaços infinitesimais do perímetro da área média vai ser o próprio perímetro da área média :
Dessa forma, o nosso ângulo de torção vai ficar assim:
Substituindo os valores:
- ;
- ;
- ;
- ;
- ;
- & ,
E calculando tudo, encontramos que:
A maioria dos professores prefere que os resultados finais sejam dados em graus (), então vamos fazer a conversão do ângulo acima de radianos para graus!
Para tanto, podemos perceber que:
Ou seja:
Substituindo isso no ângulo de torção encontrado, temos que:
Calculando isso, encontramos nossa resposta para a segunda e última parte do exercício:
Resposta
Exercício Resolvido #2
Russell Charles Hibbeler, Resistência dos Materiais, 7ª ed. São Paulo: Pearson Prentice Hall, 2010, pp. 164-5.102.
Um tubo com as dimensões mostradas na figura é submetido a um torque . Despreze as concentrações de tensão em seus cantos, determine a tensão de cisalhamento média no tubo nos pontos e .
Passo 1
O que está acontecendo?
O tubo de paredes finas retangular possui dimensões conforme a figura abaixo:
Da figura, conseguimos ver como o tubo possui dimensões médias de e de :
Consequentemente, o tubo possui uma área média :
Além disso, também da figura, conseguimos ver que o tubo possui, na região do ponto , uma espessura e, na região do ponto , uma espessura .
Um torque é aplicado no tubo.
E o que é que o exercício quer?
Ele quer que a gente determine as tensões de cisalhamento médias nos pontos e do tubo, que vão ser dadas pela fórmula:
Passo 2
Então primeiro, vamos começar calculando a tensão de cisalhamento média no ponto .
Aplicando a fórmula de para , temos que:
Substituindo os valores:
- ;
- ;
- & ,
- ;
- ;
- & ,
Encontramos que:
Mas, como é o mesmo que , isso significa que:
Passo 3
Em seguida, vamos calcular a tensão de cisalhamento média no ponto .
Aplicando a fórmula de para , temos:
Substituindo:
Encontramos que:
E assim terminamos o exercício!
Resposta
Exercício Resolvido #3
Elaboração própria
Deseja-se construir um tubo de parede fina com espessura das paredes constantes. Sabendo que o tubo é retangular e possui as dimensões mostradas abaixo, determine o valor da espessura do tubo sabendo que o material que ele é feito possui tensão de cisalhamento admissível de e o local em que ele será usado apresentará esforços torsores de
OBS:. PARA EFEITO DE CÁLCULO. Como consideramos espessuras de paredes finas para o nosso caso, qualquer valor de espessura que esteja sujeito a equação pode ser desprezado por representar um valor muito pequeno.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor de , que é dado no enunciado
Também determinamos facilmente o valor da tensão cisalhante média, como queremos a espessura máxima que o nosso tubo pode ter, queremos exatamente o valor limite que poderia causar o rompimento da peça, como isso temos que fazer
Agora para determinarmos os outros valores devemos tomar um certo cuidado, pois estamos falando que tanto a área média quanto a própria espessura são valores que não conhecemos, vamos analisar então cuidadosamente.
Passo 2
Precisamos agora determinar a nossa área média, como sabemos a área média é dada pela área da figura quando tomamos como medida a metade de espessura de cada lado, como mostra a figura baixo, ou seja, podemos definir a nossa área média como
Substituindo isso na nossa equação principal teremos que
Como temos no nosso enunciado que podemos desprezar o valor de teremos a seguinte equação
Como sabemos a nossa equação do segundo grau apresentará duas soluções, e a resposta mais adequada será a que possuir o menor valor de espessura, solucionando a nossa equação teremos que
Logo a espessura mais fina que o nosso tubo poderá ter é de
Como queremos trabalhar com valores usuais para quem fará o tubo, aproximaremos o valor para meio centímetro, ou seja
Resposta
(valor calculado)
(valor usual)
Exercício Resolvido #4
Elaboração própria
Abaixo é dado um tubo de parede fina com seção circular. Sabendo que ele foi sujeito ao torque mostrado, determine o valor da tensão cisalhante média para esse tubo.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor de , que é dado no enunciado
Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por
Agora precisamos determinar o valor da área média do nosso tubo.
Passo 2
Precisamos agora determinar a nossa área média, como sabemos a área média é dada pela área da figura quando tomamos como medida a metade de espessura de cada lado, como mostra a figura baixo, ou seja, podemos definir a nossa área média como
Lembrando que
Substituindo isso na nossa equação principal teremos que
Resposta
Exercício Resolvido #5
Elaboração própria
Um tubo de aço com tensão cisalhante admissível igual a , foi sujeito a um torque . Sabendo que a espessura desse tubo é de 5mm e que o raio externo do mesmo é de 60 cm, determine o torque máximo que podemos aplicar nesse tubo sem que ocorra o rompimento do mesmo.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor do , que é dado no enunciado
Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por
Agora precisamos determinar o valor da área média do nosso tubo.
Passo 2
Precisamos agora determinar a nossa área média, como sabemos a área média é dada pela área da figura quando tomamos como medida a metade de espessura de cada lado, como mostra a figura baixo, ou seja, podemos definir a nossa área média como
ou
Lembrando que
Substituindo isso na nossa equação principal teremos que
Resposta
Exercício Resolvido #6
Elaboração própria
Em uma estrutura foi necessário utilizar um tubo de paredes finas de perfil I, como vemos na figura abaixo. Quando projetado, o tubo deveria apresentar espessuras de paredes constante, porém o resultado final foi que a espessura da parede da região central é metade da espessura da parede da região superior e inferior. Sabendo que a espessura da parede da região superior e inferior são exatamente iguais valendo nesse caso 1mm. E que ainda a peça foi sujeita a um torque de , determine o valor da tensão cisalhante média que ocorre nesse tubo nos pontos A, B, C e D.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor de , que é dado no enunciado
Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por
Sabemos que a região central tem paredes com espessuras com metade da espessura da parede de cima e de baixo, logo teremos que
Agora precisamos determinar o valor da área média do nosso tubo.
Passo 2
Para determinarmos a área média do nosso tubo, precisaremos definir 3 regiões de cálculo para não errarmos bobeira, então vamos lá.
Primeiro vamos fazer a divisão das regiões.
Olhando as medidas dos lados que farão parte da área média teremos que
Lembrando que
Teremos que as áreas serão
Logo a área média será
Substituindo isso na nossa equação principal teremos que
Resposta
Exercício Resolvido #7
Elaboração própria
Um tubo de parede fina possui seção T como mostrado na figura. Sabe-se que a tensão cisalhante admissível desse material é de . Também sabemos que a espessura da parede é constante por todo o tubo e vale 0,1mm. Sabendo isso determine o valor do toque máximo que podemos aplicar nessa peça sem que ela rompa.
Passo 1
Como podemos notar, se trata de um problema relacionando a tubos de paredes finas quando ocorre torção dos elementos, sabemos que nesse tipo de questão devemos usar a fórmula
Alguns valores determinamos facilmente, por exemplo o valor do , que é dado no enunciado
Também determinamos facilmente o valor da espessura do nosso tubo, que é dada por
Agora precisamos determinar o valor da área média do nosso tubo.
Passo 2
Para determinarmos a área média do nosso tubo, precisaremos definir 2 regiões de cálculo para não errarmos bobeira, então vamos lá.
Primeiro vamos fazer a divisão das regiões.
Olhando as medidas dos lados que farão parte da área média teremos que
Lembrando que
Teremos que as áreas serão
Logo a área média será
Substituindo isso na nossa equação principal teremos que