Conceito
Teoria
Introdução
Toda estrutura possui uma definição, no nosso caso queremos definir duas coisas. A primeira é: o que é uma viga. A segunda é a mais importante de todas: como o meu professor cobra isso na minha prova?
vale lembrar que na aula de esforços internos em vigas, no assunto flexão, temos o passo a passo para resolver vigas por um método que usa equilíbrio, no assunto vigas vamos definir exatamente como identificar as nossas vigas e na aula soluções de vigas simples iremos aprender um método por integrais que assim como o método de equilíbrio nos ajuda a determinar os esforços internos na nossa viga, mas nesse caso estaremos calculando diretamente a fórmula pelas integrais. Vamos então definir o que é a nossa viga?
O que são as vigas e as estruturas com varias vigas ou barras?
A viga, ou barra, pode ser definida como um elemento simples da nossa estrutura, quando ela está diretamente ligada aos apoios e analisamos ela apenas em um sentido, definimos ela como viga da nossa estrutura, sendo que iremos analisar nela apenas os esforços que agem sobre ela. Quando está ligada a outras barras e analisamos barras diferentes em sentidos diferentes, nesse caso definimos que o nosso conjunto de barras formam outras estruturas, como treliças, pórticos, grelhas e vigas Gerber, por exemplo. Aqui em baixo vemos alguns exemplos
Podemos ver que nesse caso temos apenas a nossa viga, que já veremos como saber se ela é isostática, hipostática ou ainda hiperestática. Mas perceba que se trata apenas de uma viga ligada diretamente aos apoios, que analisaremos apenas a ação das cargas sobre ela, e a partir dessas cargas faremos a avaliação dos diagramas de Normal, Cortante e Momento fletor, ou seja, não temos ação de outras barras, ou outras estruturas.
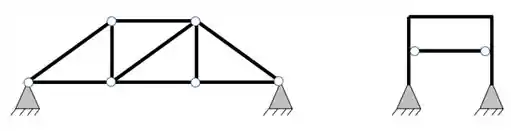
Já nesse caso nós temos um conjunto de barras, que não atuam separadamente, mas que são cruciais para o funcionamento da estrutura e que afetaram umas as outras no que se refere ao diagrama de momentos fletores, cortantes e normais. Por isso nesse caso definimos os nossos conjuntos de barras com outro nome. Sendo nesse caso, o primeiro grupo de barras as treliças e o segundo grupo, os pórticos.
Por fim, ainda temos um terceiro grupo de estruturas, que parece muito com uma viga simples, mas que nesse caso se trata de um conjunto de vigas e apoios, que podem ser estudados e analisados de forma separada quando fizermos alguns cálculos. Nesse caso, nos chamamos esse conjunto de barras de viga mesmo, mas com um nome especial, Vigas Gerber.
O que o professor pode pedir na prova com relação as vigas?
Com relação as vigas os professores podem pedir duas coisas.
- Principalmente diagrama de cortante e momento fletor, sendo muito difícil pedir diagrama de normal.
- Tipo de estrutura (hipostática, isostática e hiperestática)
- Reações de apoio também são formas que os professores adoram pedir nas provas
- Por fim, fórmula do cortante e do momento fletor.
De todos os pontos levantados acima, nós vamos analisar nessa aula como definir o tipo de estrutura. Os outros 3 pontos iremos analisar na aula de soluções de vigas simples.
Vamos lá então.
Tipos de estruturas
Para definir o tipo de estrutura é importante ter em mente 2 coisas:
- Primeiro temos que saber que apoios sempre nos darão incógnitas para o problema
- Segundo, rótulas sempre nos darão equações para o problema, lembrando que 1 rótula, em vigas, sempre nós dará uma equação quando tiverem duas barras saindo dela. Vale lembrar também que além das equações das rótulas, nós temos as equações de equilíbrio que sempre vão existir, então sempre contabilizaremos elas.
Entendido esses dois pontos, vamos ver 3 exemplos para podermos pegar o macete para sabermos o tipo de estrutura do nosso problema.
Exemplos
Temos então 3 exemplos aqui em baixo para entendermos o que devemos fazer, como eu disse ali em cima, a rótula sempre vai nos dar, no caso de vigas, mais uma equação. Nesse caso como não há rótulas, podemos ficar tranquilos quanto a isso.
Apesar de não termos rótulas temos apoios, e para sabermos o que cada apoio nos dá de incógnitas precisamos conhece-los, com isso temos que saber que
- Esse cara é um apoio do primeiro gênero, e sempre nos dará 1 incógnita
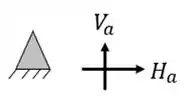
- Esse cara é um apoio do segundo gênero, e sempre nos dará 2 incógnitas
- E por fim, esse cara é um apoio do terceiro gênero, e sempre nos dará 3 incógnitas
- Exemplo 1
- Exemplo 2
- Exemplo 3
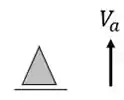
Com isso conseguimos determinar o número de incógnitas de cada um dos exemplos
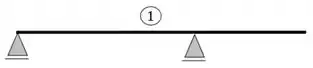
No exemplo 1 temos dois apoios de primeiro gênero, como cada um dá 1 incógnita, temos 2 incógnitas nesse exemplo.
No exemplo 2 temos um apoio do primeiro gênero e um apoio do segundo gênero, como o primeiro dá 1 incógnita e o segundo dá 2 incógnitas, temos 3 incógnitas nesse exemplo.
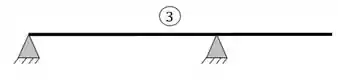
No exemplo 3 temos dois apoios do segundo gênero, como cada um dá 2 incógnitas, temos 4 incógnitas nesse exemplo.
Sabemos também que sempre temos 3 equações de equilíbrio:
E como não temos rótulas esse é o total de equações do nosso problema.
Estruturas hipostáticas
Uma estrutura hipostática é uma estrutura que ou todos os vetores dos apoios apontam na mesma direção, ou que tem o número de incógnitas inferior ao número de equações. Esse tipo de estrutura é muito ruim, pois não suporta todos os tipos de solicitações que forem aplicadas nelas. No nosso exemplo seria a estrutura 1
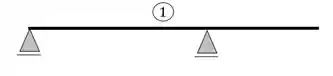
- Todos os vetores apontam na mesma direção
- 2 incógnitas
- Logo, nosso exemplo 1 é uma estrutura hipostática
Estruturas isostáticas
Uma estrutura isostática é uma estrutura que temos pelo menos um vetor em cada direção, e que o número de incógnitas é exatamente igual ao número de equações. Nesse caso a estrutura suporta todos os carregamentos postos nela.
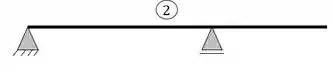
- Pelo menos um vetor em cada direção
- 3 incógnitas = 3 equações
- Logo, nosso exemplo 2 é uma estrutura isostática
Estruturas hiperestáticas
Uma estrutura hiperestática é uma estrutura que temos pelo menos um vetor em cada direção, e que o número de incógnitas é maior que o número de equações. Nesse caso a estrutura suporta todos os carregamentos postos nela
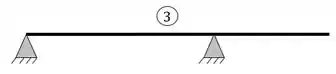
- Pelo menos um vetor em cada direção
- 4 incógnitas > 3 equações
- Logo, nosso exemplo 3 é uma estrutura hiperestática
Agora que entendemos como definir e identificar a nossa estrutura, os seus apoios e tipo estrutural da nossa viga, vamos treinar esses conceitos no exercício, e partir para o próximo tópico onde o bicho vai pegar, bora lá então.
O que o professor pode pedir na prova com relação as vigas?
Tipos de estruturas
Exemplos
Estruturas hipostáticas
Estruturas isostáticas
Estruturas hiperestáticas
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Abaixo são dados dois exemplos de vigas estruturais.
Com base em seus conhecimentos defina se essas estruturas são Isostáticas, hiperestáticas ou ainda hipostáticas. Caso as estruturas sejam definidas como os dois últimos casos antes mencionado, determine maneiras de transformamos elas em estruturas isostáticas.
Passo 1
Fala aí, galerinha. Vamos começar definindo nossas vigas!!!
Pra saber se uma estrutura é isostática, hipostática ou hiperestática, nós precisamos calcular o número de equações e o número de incógnitas. A equações são as equações de equilíbrio. E as incógnitas são as reações de apoio da nossa estrutura.
Se o número de incógnitas é MENOR que o número de equações, a estrutura é HIPOSTÁTICA!
Se o número de incógnitas é IGUAL ao número de equações, a estrutura é ISOSTÁTICA!
Se o número de incógnitas é MAIOR que o número de equações, a estrutura é HIPERESTÁTICA!
Na nossa estrutura 1, temos 2 incógnitas referentes ao apoio de segundo gênero e, para cada apoio de primeiro gênero, temos mais 1 incógnita. Então ao todo temos 4 incógnitas (reações de apoio). Como sempre, nós temos 3 equações da estática, mas, nesse caso, teremos mais 1 por causa da rótula. Para cada rótula, ganhamos mais 1 equação, pois o somatório de momentos na rótula é igual a zero. Então isso quer dizer que temos o mesmo número de equações e incógnitas, ou seja, nossa estrutura 1 é ISOSTÁTICA!
Na nossa estrutura 2, temos 5 reações de apoio (2 do apoio de segundo gênero e mais 1 pra cada apoio de primeiro gênero). E como temos 3 rótulas, vamos ter mais 3 equações além das 3 equações de equilíbrio. Então ao todo temos 5 incógnitas e 6 equações, esse é um caso de estrutura HIPOSTÁTICA!
Passo 2
A questão também pede pra gente dizer formas de transformar as vigas hipostáticas ou hiperestáticas em vigas isostáticas. Pra primeira, não vamos precisar. Vamos ver como vai ficar isso pra segunda!
Na verdade, isso é bem simples. Uma forma de aumentar o número de incógnitas é transformar os apoios. Na figura abaixo trocamos o apoio mais à direita, que era de primeiro gênero, por um apoio de segundo gênero. Mas também poderíamos ter trocado um dos apoios centrais, em vez desse último. Também poderíamos ter trocado o apoio de segundo gênero por um engaste e deixar os de primeiro gênero como estão, porque o apoio de terceiro gênero tem 3 reações de apoio e então elas totalizariam 6 incógnitas.
Em vez de aumentar o número de incógnitas também podemos diminuir o número de equações. E o jeito de fazer isso é retirando rótulas. Como só temos uma equação a mais que o número de incógnitas, tiramos a rótula do meio. Mas poderíamos ter tirado qualquer uma das 3 que também daria certo.
Essa forma de resolver, trocando apoios e rótulas também pode ser usado para as estruturas hiperestáticas. Mas aí fica ao contrário. Nas hiperestáticas, vamos adicionar rótulas (pra aumentar o número de equações) ou quebrar vínculos dos apoios transformando em apoios mais simples (para diminuir o número de incógnitas). Você vai ver muito disso mais pra frente no assunto de estruturas hiperestáticas!
Resposta
A viga 1 é isostática.
A viga 2 é hipostática. Para transformá-la em isostática podemos retirar 1 rótula ou trocar 1 dos apoios por uma opção mais restritiva.
Exercício Resolvido #2
Elaboração Própria
Paras a viga Compostas abaixo, faça a separação correta em vigas simples indicando onde ficaram os apoios fictícios e para onde serão transferidas as suas reações de apoios.
Passo 1
Sempre que estivermos em um caso de separação de vigas, devemos fazer o seguinte
- Primeiro e mais importante, devemos fazer a separação SEMPRE quebrando nas rótulas, nunca, em outros trechos.
- Quando quebrar uma rótula deve-se analisar o seguinte, o apoio fictício que aparece nela, terá para onde transferir essa reação e manter a estrutura que ele está isostática? Se a resposta for sim, então cortamos a rótula corretamente, se for não, provavelmente escolhemos a estrutura errada, ou, de fato, essa rótula não pode ser retirada.
- Analisamos se todas as estruturas são isostáticas, se forem, a separação está correta, se não forem devemos ver o seguinte. Ou a separação foi feita errada, ou, a estrutura não é isostática
- Por fim, analisamos a ordem de solução da nossa viga, o que facilita na hora de fazer os cálculos.
Entendido isso, podemos ir para o exercício, para colocarmos em pratica o nosso passo a passo. Vamos lá? Sigam-me os Bons!!
Passo 2
Vamos lá então, como vimos, precisamos quebrar as rótulas, e avaliar quais seriam as barras mais aptas a receberem os apoios fictícios, e qual barra se apoia em qual, vamos fazer isso então, quebrando as rótulas teremos que
Sabemos então que agora temos barras separadas, e elas ficaram separadas da seguinte maneira, e com os seguintes nomes
Mas como escolher os apoios fictícios?
O macete é ver quem já está equilibrado e descartar, nesse caso as vigas 1 e 3 já são auto equilibradas, pois a viga 1 tem 3 incógnitas e 3 equações, assim como a viga 3 que também tem 3 incógnitas e 3 equações, ou seja, nos trechos que quebramos as suas rótulas não colocaremos apoios fictícios.
Porém veja que as barras 2 e 4 não estão equilibradas, e tanto uma quanto a outra possuíam rótulas que quebramos, com isso, será mais usual colocar os apoios fictícios nelas.
Passo 3
Colocando os apoios fictícios nas barras 2 e 4, onde quebramos as rótulas e numerando os apoios fictícios, teremos,
Perceba o seguinte, a viga 4 passou a ser estável, se tornando isostática quando analisamos ela com o apoio fictício. A viga 2 devemos tomar um cuidado, pelo balanceamento de incógnitas, ela é uma viga hiperestática, porém, em vigas, sempre consideraremos cargas verticais, ou seja, não haverá reação de apoio horizontal, se não há reação de apoio horizontal, podemos considerar, nesse caso especifico de apoio fictícios, uma viga isostática, apenas para fins de cálculo.
Também devemos ver o seguinte
- Apoio 1 transfere suas reações, com sinal invertido, para a viga 1
- Apoio 2 transfere suas reações, com sinal invertido, para a viga 3
- Apoio 3 transfere suas reações, com sinal invertido, para a viga 3
Passo 4
Veja que seguimos o nosso passo a passo,
- Primeiro quebramos as rótulas e separamos as vigas.
- Depois avaliamos onde ficariam os apoios fictícios e vimos que todas as rótulas foram cortadas corretamente.
- No final do segundo passo, avaliamos se todas as estruturas eram isostáticas, e de fato eram.
Agora só falta o último passo:
Definir a ordem de solução, e essa ordem é bem simples, basta ver o seguinte, quem tem apoio fictício, sempre é resolvido primeiro, quem recebe as reações dos apoios fictícios, são resolvidas posteriormente, com isso teremos a seguinte ordem de solução
Pois a barra 2 possui mais apoios fictícios, em seguida
Após resolver o primeiro, o segundo a ter mais apoios fictícios passa a ser a barra 4, que é a segunda a ser resolvida. Tendo em mãos todas as reações de apoio fictício, transferimos elas para as suas barras corretas, seguindo a ordem do final do passo 2. Tomar cuidado pois essas reações vão para as suas barras correspondentes com os sinais invertidos, ou melhor, o sentido dos vetores calculados será contraria a direção calculada, feito isso, a próxima sequencia de solução será
E com isso cumprimos o que foi pedido no exercício. Separamos as vigas, conferimos se todas são isostáticas, colocamos os respectivos apoios fictícios, e por fim definimos a ordem de solução. Show? Vamos para o próximo exercício então.
Resposta
As vigas separadas e a ordem de solução será
Exercício Resolvido #3
Elaboração Própria
Abaixo temos uma viga de ponte, representada pelo seu diagrama unifilar, possuindo um trecho Gerber. Usando seus conhecimentos de separação de vigas, determine quais serão os trechos separados dessa viga, assim como seus apoios fictícios.
Passo 1
Sempre que estivermos em um caso de separação de vigas, devemos fazer o seguinte
- Primeiro e mais importante, devemos fazer a separação SEMPRE quebrando nas rótulas, nunca, em outros trechos.
- Quando quebrar uma rótula deve-se analisar o seguinte, o apoio fictício que aparece nela, terá para onde transferir essa reação e manter a estrutura que ele está isostática? Se a resposta for sim, então cortamos a rótula corretamente, se for não, provavelmente escolhemos a estrutura errada, ou, de fato, essa rótula não pode ser retirada.
- Analisamos se todas as estruturas são isostáticas, se forem, a separação está correta, se não forem devemos ver o seguinte. Ou a separação foi feita errada, ou, a estrutura não é isostática
- Por fim, analisamos a ordem de solução da nossa viga, o que facilita na hora de fazer os cálculos.
Entendido isso, podemos ir para o exercício, para colocarmos em pratica o nosso passo a passo. Vamos lá? Sigam-me os Bons!!
Passo 2
Vamos lá então, como vimos, precisamos quebrar as rótulas, e avaliar quais seriam as barras mais aptas a receberem os apoios fictícios, e qual barra se apoia em qual, vamos fazer isso então, quebrando as rótulas teremos que
Sabemos então que agora temos barras separadas, e elas ficaram separadas da seguinte maneira, e com os seguintes nomes
Mas como escolher os apoios fictícios?
O macete é ver quem já está equilibrado e descartar, nesse caso as vigas 2 e 4 já são auto equilibradas, pois a viga 2 tem 3 incógnitas e 3 equações, porém a viga 4 tem 2 incógnitas e 3 equações, mas lembre-se que em vigas consideramos apenas cargas verticais, sendo ignorado a existência de carregamento horizontal, o que faz com que uma das equações saiam e passemos a ter 2 equações e 2 incógnitas, o que caracteriza que a nossa viga seja isostática, ou seja, nos trechos que quebramos as suas rótulas não colocaremos apoios fictícios.
Porém veja que as barras 1 ,3 e 5 não estão equilibradas, e tanto uma quanto a outra possuíam rótulas que quebramos, com isso, será mais usual colocar os apoios fictícios nelas.
Passo 3
Colocando os apoios fictícios nas barras 1,3 e 5, onde quebramos as rótulas e numerando os apoios fictícios, teremos,
Perceba o seguinte, a viga 1 e 5 passaram a ser estáveis, se tornando isostáticas quando analisamos elas com os apoios fictícios. A viga 3 devemos tomar um cuidado, pelo balanceamento de incógnitas, ela é uma viga hiperestática, porém, em vigas, sempre consideraremos cargas verticais, ou seja, não haverá reação de apoio horizontal, se não há reação de apoio horizontal, podemos considerar, nesse caso especifico de apoio fictícios, uma viga isostática, apenas para fins de cálculo.
Também devemos ver o seguinte
- Apoio 1 transfere suas reações, com sinal invertido, para a viga 2
- Apoio 2 transfere suas reações, com sinal invertido, para a viga 2
- Apoio 3 transfere suas reações, com sinal invertido, para a viga 4
- Apoio 4 transfere suas reações, com sinal invertido, para a viga 4
Passo 4
Veja que seguimos o nosso passo a passo,
- Primeiro quebramos as rótulas e separamos as vigas.
- Depois avaliamos onde ficariam os apoios fictícios e vimos que todas as rótulas foram cortadas corretamente.
- No final do segundo passo, avaliamos se todas as estruturas eram isostáticas, e de fato eram.
Agora só falta o último passo:
Definir a ordem de solução, e essa ordem é bem simples, basta ver o seguinte, quem tem apoio fictício, sempre é resolvido primeiro, quem recebe as reações dos apoios fictícios, são resolvidas posteriormente, com isso teremos a seguinte ordem de solução
Pois a barra 3 possui mais apoios fictícios, em seguida
Após resolver o primeiro, o segundo a ter mais apoios fictícios passam a ser as barras 1 e 5, que são as segundas a serem resolvidas. Tendo em mãos todas as reações de apoio fictício, transferimos elas para as suas barras corretas, seguindo a ordem do final do passo 2. Tomar cuidado pois essas reações vão para as suas barras correspondentes com os sinais invertidos, ou melhor, o sentido dos vetores calculados será contrário ao sentido calculado, feito isso, a próxima sequência de solução será
E com isso cumprimos o que foi pedido no exercício. Separamos as vigas, conferimos se todas são isostáticas, colocamos os respectivos apoios fictícios, e por fim definimos a ordem de solução. Show? Vamos para o próximo exercício então.
Resposta
As vigas separadas e a ordem de solução será
Exercício Resolvido #4
Elaboração Própria
Paras a viga Compostas abaixo, faça a separação correta em vigas simples indicando onde ficaram os apoios fictícios e para onde serão transferidas as suas reações de apoios.
Passo 1
Sempre que estivermos em um caso de separação de vigas, devemos fazer o seguinte
- Primeiro e mais importante, devemos fazer a separação SEMPRE quebrando nas rótulas, nunca, em outros trechos.
- Quando quebrar uma rótula deve-se analisar o seguinte, o apoio fictício que aparece nela, terá para onde transferir essa reação e manter a estrutura que ele está isostática? Se a resposta for sim, então cortamos a rótula corretamente, se for não, provavelmente escolhemos a estrutura errada, ou, de fato, essa rótula não pode ser retirada.
- Analisamos se todas as estruturas são isostáticas, se forem, a separação está correta, se não forem devemos ver o seguinte. Ou a separação foi feita errada, ou, a estrutura não é isostática
- Por fim, analisamos a ordem de solução da nossa viga, o que facilita na hora de fazer os cálculos.
Entendido isso, podemos ir para o exercício, para colocarmos em pratica o nosso passo a passo. Vamos lá? Sigam-me os Bons!!
Passo 2
Vamos lá então, como vimos, precisamos quebrar as rótulas, e avaliar quais seriam as barras mais aptas a receberem os apoios fictícios, e qual barra se apoia em qual, vamos fazer isso então, quebrando as rótulas teremos que
Sabemos então que agora temos barras separadas, e elas ficaram separadas da seguinte maneira, e com os seguintes nomes
Mas como escolher os apoios fictícios?
O macete é ver quem já está equilibrado e descartar, nesse caso as vigas 1 e 3 já são auto equilibradas, pois a viga 1 tem 2 incógnitas e 2 equações, lembrando que como se trata de vigas descartamos os esforços horizontais, assim como a viga 3 que também tem 3 incógnitas e 3 equações, ou seja, nos trechos que quebramos as suas rótulas não colocaremos apoios fictícios.
Porém veja que a barra 2 não está equilibrada, e ela possui rótulas que quebramos, com isso, será mais usual colocar os apoios fictícios nelas.
Passo 3
Colocando os apoios fictícios na barra 2, onde quebramos as rótulas e numerando os apoios fictícios, teremos,
Perceba o seguinte, a viga 2 passou a ser estável, se tornando isostática quando analisamos ela com o apoio fictício.
Também devemos ver o seguinte
- Apoio 1 transfere suas reações, com sinal invertido, para a viga 1
- Apoio 2 transfere suas reações, com sinal invertido, para a viga 3
Passo 4
Veja que seguimos o nosso passo a passo,
- Primeiro quebramos as rótulas e separamos as vigas.
- Depois avaliamos onde ficariam os apoios fictícios e vimos que todas as rótulas foram cortadas corretamente.
- No final do segundo passo, avaliamos se todas as estruturas eram isostáticas, e de fato eram.
Agora só falta o último passo:
Definir a ordem de solução, e essa ordem é bem simples, basta ver o seguinte, quem tem apoio fictício, sempre é resolvido primeiro, quem recebe as reações dos apoios fictícios, são resolvidas posteriormente, com isso teremos a seguinte ordem de solução
Tendo em mãos todas as reações de apoio fictício, transferimos elas para as suas barras corretas, seguindo a ordem do final do passo 2. Tomar cuidado pois essas reações vão para as suas barras correspondentes com os sinais invertidos, ou melhor, o sentido dos vetores calculados será contraria a direção calculada, feito isso, a próxima sequência de solução será
E com isso cumprimos o que foi pedido no exercício. Separamos as vigas, conferimos se todas são isostáticas, colocamos os respectivos apoios fictícios, e por fim definimos a ordem de solução. Show? Vamos para o próximo exercício então.
Resposta
As vigas separadas e a ordem de solução será
Exercício Resolvido #5
Elaboração Própria
Paras a viga Compostas abaixo, faça a separação correta em vigas simples indicando onde ficaram os apoios fictícios e para onde serão transferidas as suas reações de apoios.
Passo 1
Sempre que estivermos em um caso de separação de vigas, devemos fazer o seguinte
- Primeiro e mais importante, devemos fazer a separação SEMPRE quebrando nas rótulas, nunca, em outros trechos.
- Quando quebrar uma rótula deve-se analisar o seguinte, o apoio fictício que aparece nela, terá para onde transferir essa reação e manter a estrutura que ele está isostática? Se a resposta for sim, então cortamos a rótula corretamente, se for não, provavelmente escolhemos a estrutura errada, ou, de fato, essa rótula não pode ser retirada.
- Analisamos se todas as estruturas são isostáticas, se forem, a separação está correta, se não forem devemos ver o seguinte. Ou a separação foi feita errada, ou, a estrutura não é isostática
- Por fim, analisamos a ordem de solução da nossa viga, o que facilita na hora de fazer os cálculos.
Entendido isso, podemos ir para o exercício, para colocarmos em pratica o nosso passo a passo. Vamos lá? Sigam-me os Bons!!
Passo 2
Vamos lá então, como vimos, precisamos quebrar as rótulas, e avaliar quais seriam as barras mais aptas a receberem os apoios fictícios, e qual barra se apoia em qual, vamos fazer isso então, quebrando as rótulas teremos que
Sabemos então que agora temos barras separadas, e elas ficaram separadas da seguinte maneira, e com os seguintes nomes
Mas como escolher os apoios fictícios?
O macete é ver quem já está equilibrado e descartar, nesse caso as vigas 1 e 3 não são auto equilibradas, pois a viga 1 tem 1 incógnita e 3 equações, lembrando que como se trata de vigas descartamos os esforços horizontais, assim como a viga 3 que também tem 1 incógnita e 3 equações, ou seja, nos trechos que quebramos as suas rótulas não colocaremos apoios fictícios.
Passo 3
Colocando os apoios fictícios na barra 1 e 3, onde quebramos as rótulas e numerando os apoios fictícios, teremos,
Perceba o seguinte, as vigas 1 e 3 passaram a ser estáveis, se tornando isostática quando analisamos ela com o apoio fictício.
Também devemos ver o seguinte
- Apoio 1 transfere suas reações, com sinal invertido, para a viga 2
- Apoio 2 transfere suas reações, com sinal invertido, para a viga 2
Passo 4
Veja que seguimos o nosso passo a passo,
- Primeiro quebramos as rótulas e separamos as vigas.
- Depois avaliamos onde ficariam os apoios fictícios e vimos que todas as rótulas foram cortadas corretamente.
- No final do segundo passo, avaliamos se todas as estruturas eram isostáticas, e de fato eram.
Agora só falta o último passo:
Definir a ordem de solução, e essa ordem é bem simples, basta ver o seguinte, quem tem apoio fictício, sempre é resolvido primeiro, quem recebe as reações dos apoios fictícios, são resolvidas posteriormente, com isso teremos a seguinte ordem de solução
Em seguida teremos
Tendo em mãos todas as reações de apoio fictício, transferimos elas para as suas barras corretas, seguindo a ordem do final do passo 2. Tomar cuidado pois essas reações vão para as suas barras correspondentes com os sinais invertidos, ou melhor, o sentido dos vetores calculados será contraria a direção calculada, feito isso, a próxima sequência de solução será
E com isso cumprimos o que foi pedido no exercício. Separamos as vigas, conferimos se todas são isostáticas, colocamos os respectivos apoios fictícios, e por fim definimos a ordem de solução. Show? Vamos para o próximo exercício então.
Resposta
As vigas separadas e a ordem de solução será
