Uma janela de vidro de de largura e de altura apresenta de espessura e condutividade térmica de . Se as temperaturas interna e externa do vidro em um dia de inverno são e respectivamente, responda:
Qual a taxa de perda de calor através do vidro?
Para reduzir as perdas de calor através das janelas, costuma-se utilizar construções com painel duplo, em que as duas placas de vidro são separadas por ar. Se o espaçamento entre elas for de e as superfícies em contato com o ar tiver temperaturas de e , qual a taxa de perda de calor de uma janela ? A condutividade térmica do ar é .
Passo 1
a) O enunciado fala de uma janela de vidro com dimensões com temperaturas interna e externa conhecidas, como mostrado aqui no esquema:
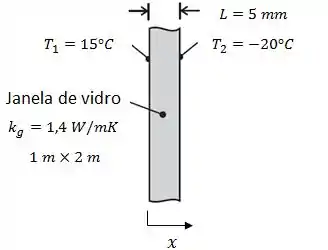
A primeira coisa que temos que fazer é encontrar a taxa de calor que passa através desse vidro. Sabemos que essa taxa é dada por:
Teremos um fluxo de calor no sentido da espessura do vidro, que definimos como eixo x. Como o calor flui do corpo mais quente para o corpo mais frio, a taxa de perca de calor acontece da esquerda para a direita, no sentido positivo do eixo x.
Passo 2
Qual a taxa de perda de calor através do vidro?
Como o calor está sendo transferido por condução através da janela, vamos usar a Lei de Fourier para determinar o fluxo de calor:
Nesse caso, como estamos trabalhando com um problema de placa plana, podemos escrever a Lei de Fourier da seguinte forma:
Juntando essa expressão com a que escrevemos no Passo 1, a taxa de transferência de calor por condução será dada por:
Como , o calor será transferido da esquerda para a direita, no sentido positivo do eixo , logo:
Onde:
Obs.: Um detalhe importante aqui! Como estamos calculando uma variação de temperatura, podemos, neste caso, utilizar a temperatura tanto em graus Celsius ou Kelvin já que, nas duas escalas o cálculo da variação de temperatura nos dará o mesmo valor.
Substituindo os valores:
Passo 3
Para reduzir as perdas de calor através das janelas, costuma-se utilizar construções com painel duplo, em que as duas placas de vidro são separadas por ar. Se o espaçamento entre elas for de e as superfícies em contato com o ar tiver temperaturas de e , qual a taxa de perda de calor de uma janela ? A condutividade térmica do ar é .
Agora que colocamos duas janelas de vidro uma do lado da outra, deixando um espaço entre elas ocupado por ar, a ideia é a seguinte:
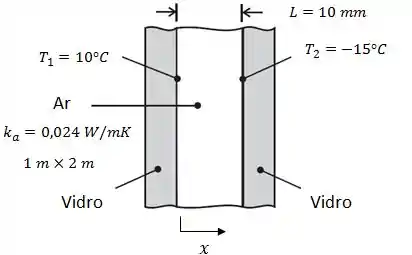
Se o objetivo é reduzir a perca de calor através da janela, então esperamos encontrar uma taxa de perda de calor menor do que encontramos na letra a. Considerando que a engenhoca funcione, teremos um cômodo mais quentinho do que no primeiro caso, certo? Logo a temperatura interna da janela deverá ser maior que 15ºC!
Então como a gente pode calcular a taxa de perda de calor se não sabemos a temperatura interna da janela? Calma, vem comigo!
Temos um regime permanente, isso quer dizer que a janela não pode nem gerar, nem acumular energia (que aqui aparece na forma de calor), logo a taxa de perda de calor através janela é igual a taxa de perda de calor através do espaço entre as placas de vidro.
E essa a gente consegue calcular!!!
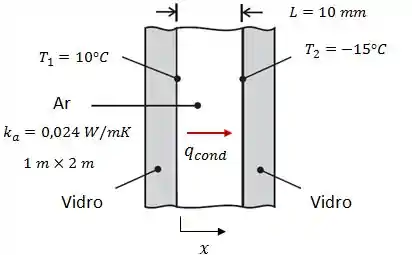
A taxa de calor transferida através do ar será:
Onde:
Substituindo os valores:
Lembrando que na letra a achamos, , que muuuuuito maior do que os 120W que terminamos de achar. Então vimos que essa engenhoca realmente funciona!!!
Resposta