Um transistor de comprimento e diâmetro é resfriado por uma corrente de ar de temperatura .
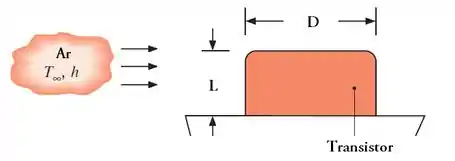
Em condições nas quais o ar mantém um coeficiente de convecção médio . Na superfície, qual a dissipação máxima de potência permitida se a temperatura da superfície não deve ultrapassar ?
Passo 1
O nosso objetivo é encontrar a taxa de calor que sai do transistor por convecção. Pelo enunciado a gente já tem informações com relação ao coeficiente de convecção (), a temperatura da superfície () e do fluido ().
Então, a gente consegue calcular o fluxo de calor pela lei de resfriamento de Newton:
Substituindo os valores:
Passo 2
Agora que já temos o fluxo, podemos calcular a taxa de dissipação da seguinte forma:
Como o problema nos deu o comprimento e o diâmetro do transistor, podemos concluir que esse cara é um cilindro. Assim, a área de troca térmica será soma da área lateral do cilindro com a área do topo com as dimensões informadas. Logo:
Onde:
Substituindo os valores:
Voltando para a taxa de dissipação: