Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método da Média Logarítmica

Ver Teoria
Exercício 41235678910

Enunciado

(Adaptado) O ar ( c p = 1005   J / k g ° C ) deve ser preaquecido por gases em um trocador de calor de escoamento cruzado antes de entrar em um forno. O ar entra no trocador de calor a 20 ° C , com na taxa de 0,8   m 3 / s , e sai a 133 ° C .

Gases de combustão ( c p = 1100   J / k g ° C ) entram a 180 ° C com uma taxa de 1,1   k g / s e saem a 95 ° C . O coeficiente global de transferência de calor baseado nos tubos é de U i n t = 120   W / m 2 . ° C .

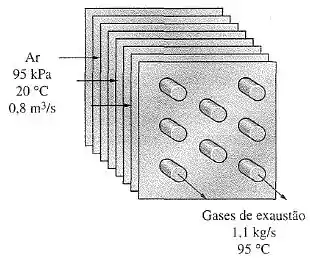
Considerando ambos os fluidos sem mistura, determine a taxa de transferência de calor e a área de troca térmica.

Passo 1

Como o problema já nos deu a vazão mássica de gás de combustão e as temperaturas de entrada e saída, a taxa de transferência de calor será dada por:

q = m ˙ . c p . T q , e n t - T q , s a i

Substituindo os valores:

q = 1,1 × 1100 × 180 - 95

Passo 2

Para calcular a superfície de transferência de calor, teremos que usar essa expressão:

q = U i n t . A i n t . Δ T l n , C F → A i n t = q U i n t . Δ T l n , C F

Agora vamos precisar calcular a média logarítmica das temperaturas!

Passo 3

Começando pela média logarítmica, temos que:

Δ T 1 = T q , e n t - T f , s a i = 180 - 133 → Δ T 1 = 47 ° C

Δ T 2 = T q , s a i - T f , e n t = 95 - 20 → Δ T 2 = 75 ° C

Logo:

Δ T m l , C F = Δ T 1 - Δ T 2 ln ⁡ Δ T 1 Δ T 2 = 47 - 75 ln ⁡ 47 75 → Δ T m l , C F = 60 ° C

Passo 4

Dessa forma, a área de troca térmica será:

A i n t = q U i n t Δ T l n , C F = 103 × 10 3 120 × 60

A i n t = 14,03   m 2

Resposta

q = 103   k W

A i n t = 14,03   m 2

Exercícios de Livros Relacionados

36 - Quando as temperaturas de saída dos fluidos em um trocador de calor não são conhecidas, ainda é prático usar o método LMTD?Explique.
Em um trocador de calor líquido-líquido de escoamento paralelo, as temperaturas de entrada e saída do fluido quente são 150 ℃ ℃ e 90 ℃ ℃, enquanto as do fluido frio são 30 ℃ ℃ e 70 ℃ ℃, respectivament
32 - A diferença entre as temperaturas dos fluidos quente e frio em um trocador de calor é dada como Δ T 1 em uma extremidade e Δ T 2 na outra extremidade.A diferença de temperatura média logarítmicaΔ
31 - Como a diferença de temperatura média logarítmica de um trocador de calor difere da diferença de temperatura média aritmética?No caso de temperaturas de entrada e saída especificadas, qual dessas
37 - Para determinadas temperaturas de entrada e de saída, para que tipo de trocador de calor Δ t l m vai ser maior: trocador de calor de tubo duplo de escoamento paralelos, tubo duplo contracorrente,