Em uma central geotérmica binária, o fluido de trabalho isobutano deve ser condensado pelo ar em um condensador a com uma taxa de . O ar entra no condensador a e deixa-o a .
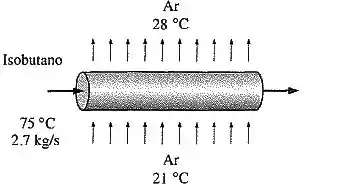
A transferência de calor com base na superfície do lado do isobutano é de . Determine a vazão mássica do ar e o coeficiente global de transferência de calor.
Passo 1
A vazão mássica de ar (fluido frio) pode ser calculada da seguinte forma:
Enquanto o coeficiente global de transferência de calor pode ser calculado por:
De qualquer forma, precisaremos da taxa de transferência de calor e da diferença de temperatura média logarítmica.
Passo 2
A taxa de transferência de calor pode ser calculada da seguinte forma:
Substituindo os valores, teremos:
![]()
Passo 3
Para a diferença de temperatura média logarítmica, teremos:
Logo:
![]()
Obs.: Como há mudança defase em um dos fluidos, o fator de correção será . Então não precisamos nos preocupar com ele nesses casos.
Passo 4
A vazão mássica de ar (fluido frio) será:
Substituindo os valores:
![]()
Passo 5
O coeficiente global de transferência de calor será:
Substituindo os valores, onde :
![]()