Um trocador de calor em escoamento cruzado não aletado é utilizado para resfriar óleo de a . O óleo entra pelos tubos a uma velocidade média igual a . São utilizados no trocador 5 tubos, com diâmetro igual a .
Ar é utilizado como fluido de resfriamento, entrando no trocador a e escoando a uma vazão de . Calcule:
O coeficiente global de troca de calor, desprezando a espessura da parede dos tubos, e considerando que o coeficiente de troca de calor externo vale .
A temperatura de saída do ar e a diferença média logarítmica de temperatura.
O comprimento dos tubos, utilizando o método da diferença média logaritmica.
Passo 1
O coeficiente global de troca de calor, desprezando a espessura da parede dos tubos, e considerando que o coeficiente de troca de calor externo vale .
Desprezando a espessura da parede dos tubos, o coeficiente global de troca de calor será calculado a partir dos coeficientes convectivos interno e externo, da seguinte forma:
Novamente, como estamos desconsiderando a espessura do tubo, . Dessa forma:
Dessa equação, temos tudo, exceto o coeficiente convectivo interno.
Passo 2
Para a convecção interna, o número de Reynolds será dado por:
Assim, como o óleo está sendo resfriado o número de Nusselt será dada por:
Dessa forma, o coeficiente convectivo interno será:
Assim, o coeficiente global de transferência de calor será:
![]()
Passo 3
A temperatura de saída do ar e a diferença média logarítmica de temperatura.
A temperatura de saída do ar pode ser calculada por:
Onde a taxa de transferência de calor é dada por:
Substituindo os valores:
Dessa forma, a temperatura de saíta do ar será:
![]()
Passo 4
A diferença média logarítmica de temperatura é dada por:
Sendo:
Assim:
![]()
Passo 5
O comprimento dos tubos, utilizando o método da diferença média logaritmica.
A taxa de transferência de calor pode ser calculada da seguinte forma:
Onde o fator de forma é calculado a partir do gráfico considerando um fluido misturado e o outro não misturado, onde:
Assim:
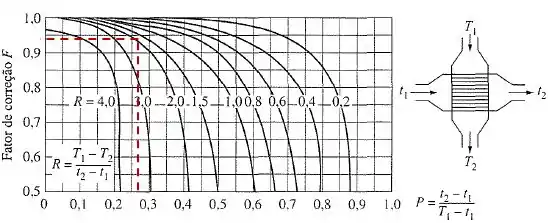
Dessa forma, o comprimento dos tubos será:
![]()
Resposta
,