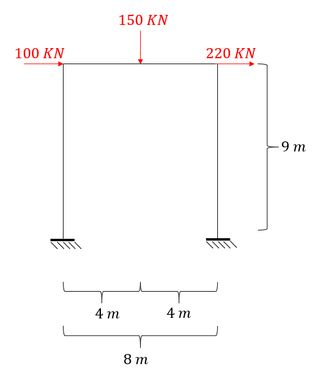
Determine o valor das reações de apoio do sistema hiperestático dado abaixo. Usar:
Passo 1
Precisamos lembrar que na primeira parte desse exercício já determinamos algumas coisas que vão ser bem importantes utilizarmos aqui. Vamos então recordar o que precisamos de mega importante da primeira parte desse exercício.
- Sistemas estruturais
- Sistema algébrico
Sabemos que definimos alguns sistemas para essa estrutura, que é dado bem aqui em baixo.
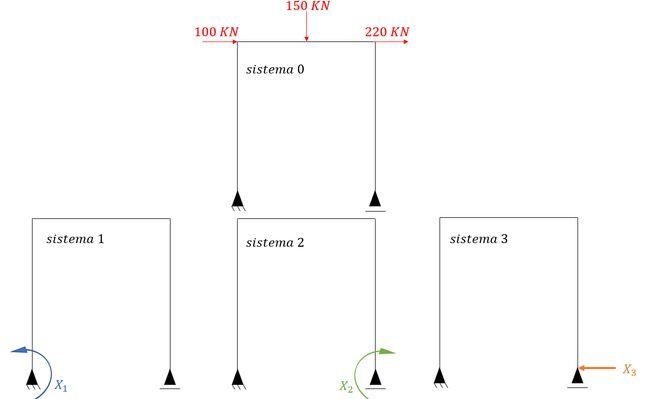
Sabemos também que nosso sistema algébrico definido foi o seguinte:
E com base nessas informações devemos calcular as nossas deformações.
Passo 2
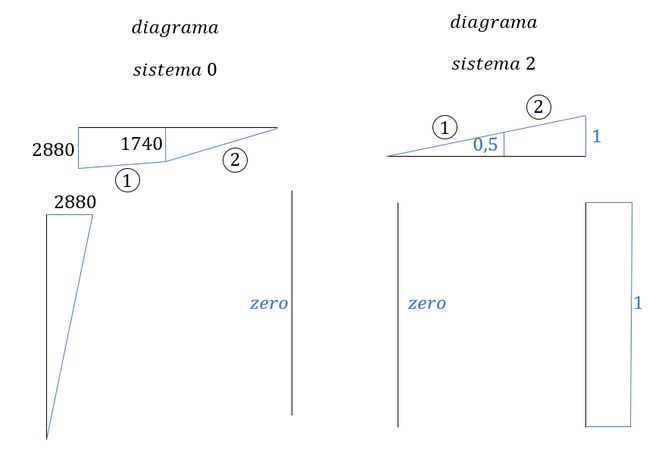
Sabemos que as deformações sempre são calculadas com base na combinação de diagramas da nossa estrutura, e no nosso caso, antes de qualquer combinação precisamos determinar os diagramas de cada um dos sistemas, então vamos lá:
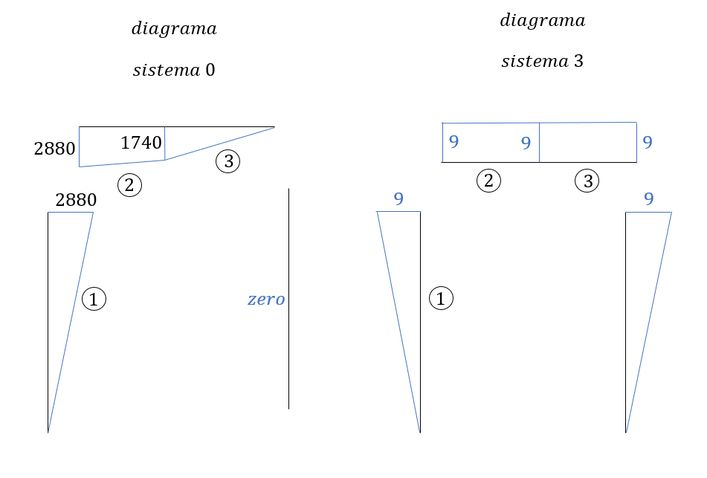
- Diagrama de momentos do sistema real
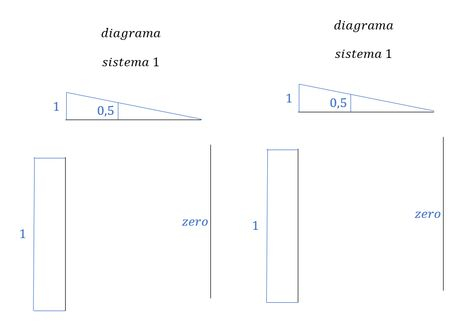
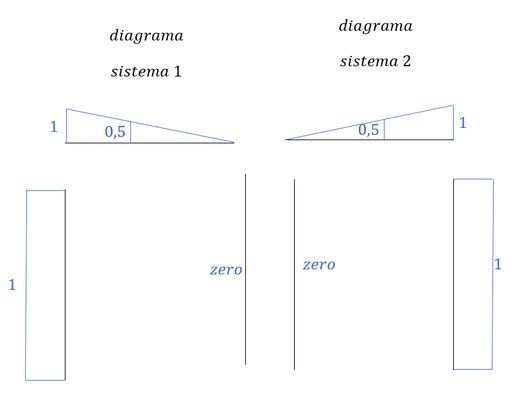
- Diagrama de momentos do sistema com a carga unitária em 1 (ou sistema 1)
- (como todas as barras da viga tem a mesma inercia podemos usar todos os valores com os valores inteiros, sem ver o quanto um é relativo ao outro). Dessa maneira precisamos combinar o diagrama real com o de carga unitária no ponto 1, assim teremos.
- Região 1
- Região 2
- Região 3
- Somando tudo
- (como todas as barras da viga tem a mesma inercia podemos usar todos os valores com os valores inteiros, sem ver o quanto um é relativo ao outro). Dessa maneira precisamos combinar o diagrama real com o de carga unitária no ponto 2, assim teremos.
- Região 1
- Região 2
- Somando tudo
- Dessa maneira precisamos combinar o diagrama 0 com o mesmo diagrama no ponto 3, assim teremos.
- Região 1
- Região 2
- Região 3
- Somando tudo
- Dessa maneira precisamos combinar o diagrama 1 com o mesmo diagrama no ponto 1, assim teremos.
- Dessa maneira precisamos combinar o diagrama 1 com o mesmo diagrama no ponto 2, assim teremos.
- Dessa maneira precisamos combinar o diagrama 1 com o mesmo diagrama no ponto 3, e vice versa, assim teremos.
- Dessa maneira precisamos combinar o diagrama 2 com o mesmo diagrama no ponto 3, e vice-versa, assim teremos.
- Dessa maneira precisamos combinar o diagrama 2 com o mesmo diagrama no ponto 2, assim teremos.
- Dessa maneira precisamos combinar o diagrama 2 com o mesmo diagrama no ponto 3, e vice-versa, assim teremos.
- Reação vertical no apoio mais esquerdo
- Reação vertical no apoio mais a direita
- Reação horizontal no apoio mais esquerdo
- Reação vertical no apoio mais esquerdo
- Reação vertical no apoio mais a direita
- Reação de momento mais a esquerda
- Reação momento mais a direita
- Reação horizontal mais a esquerda
- Reação horizontal mais a direita
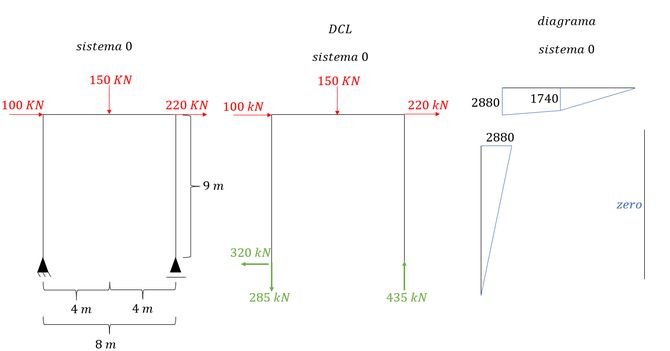
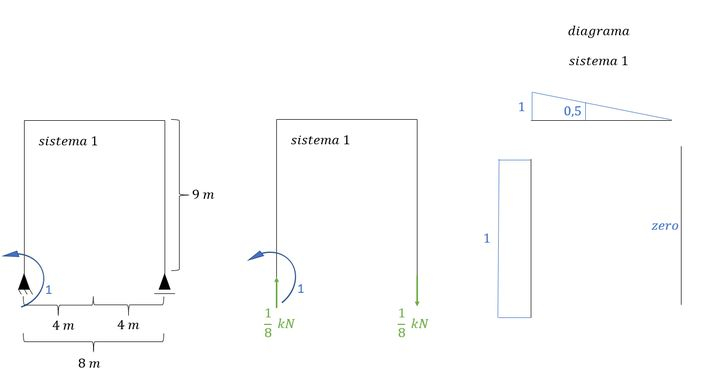
Diagrama de momentos do sistema com a carga unitária em 2 (ou sistema 2)
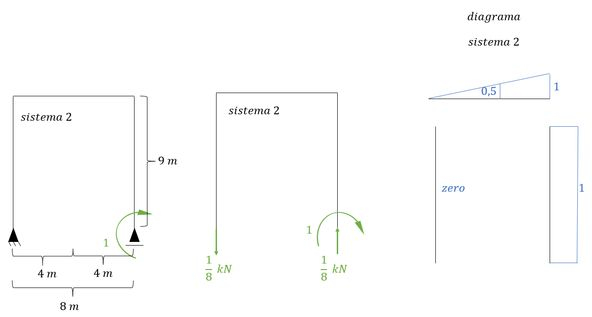
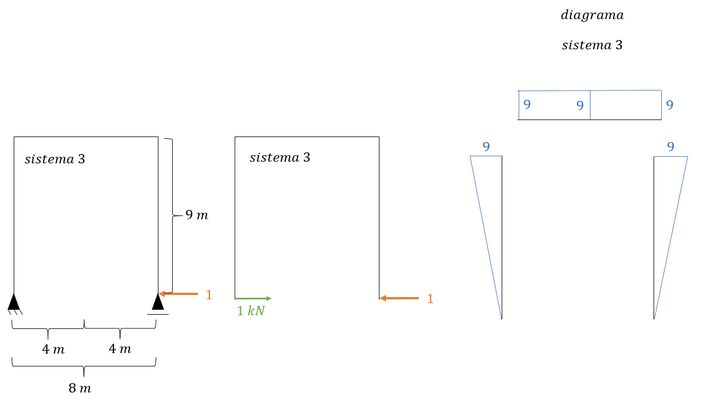
Diagrama de momentos do sistema com a carga unitária em 3 (ou sistema 3)
Passo 3
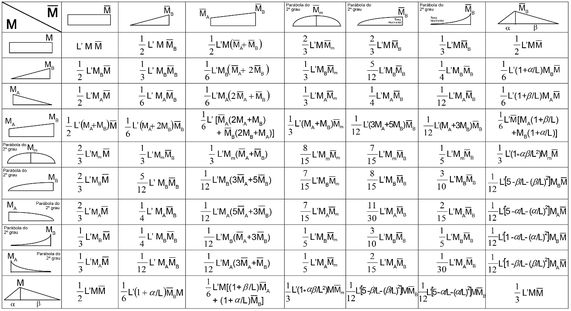
Agora, já com os diagramas em mãos precisamos determinar os deslocamentos, com isso precisamos ir combinando os nossos diagramas e ir usando a nossa tabelinha aqui de baixo:
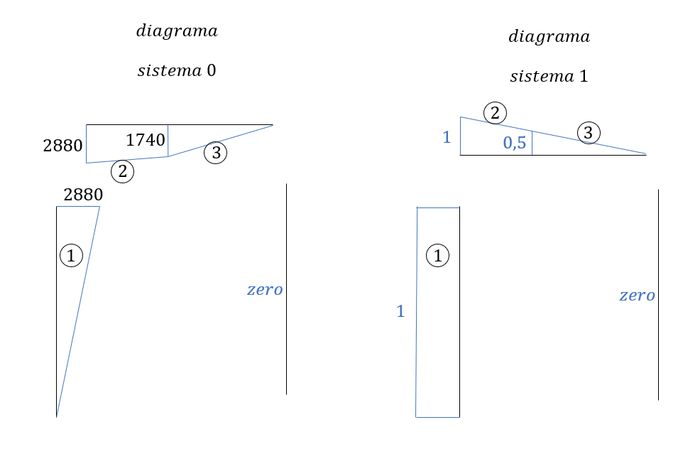
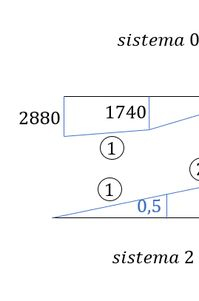
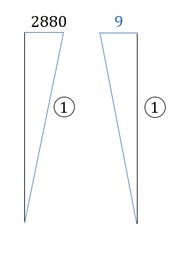
perceba que temos 3 regiões a serem combinadas, então vamos fazer uma por uma:
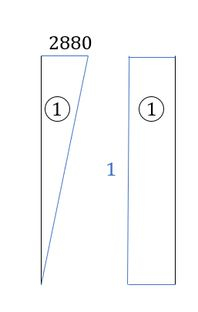
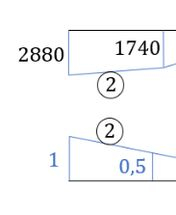
Como no enunciado temos que
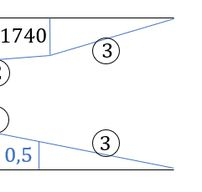
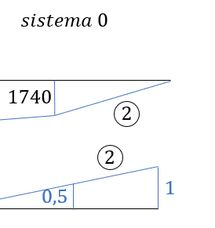
perceba que temos 2regiões a serem combinadas, e perceba que as barras verticais se anulam, então vamos fazer uma por uma:
Como no enunciado temos que
perceba que temos 3 regiões a serem combinadas, então vamos fazer uma por uma:
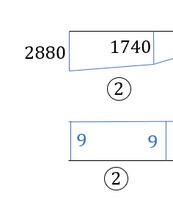
Como no enunciado temos que
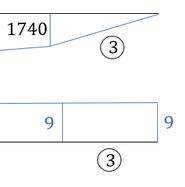
Vemos aqui que temos uma barra que irá zerar, e duas que serão completas, então vamos focar na soma dessas duas.
Como no enunciado foi dado
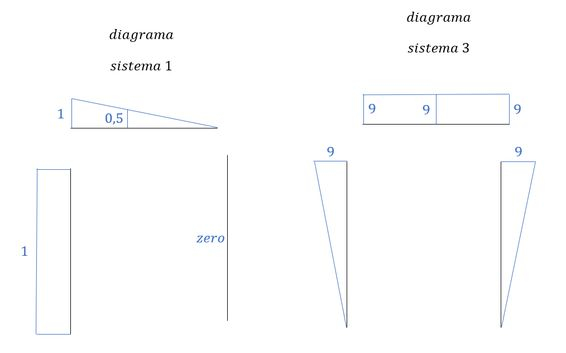
Vemos aqui que temos uma barra que irá zerar, e duas que serão completas, então vamos focar na soma dessas duas.
Como no enunciado foi dado
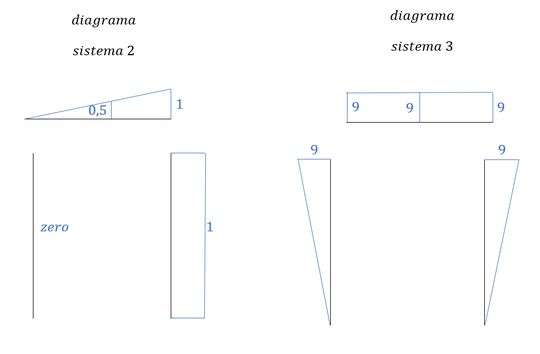
Vemos aqui que temos uma barra que irá zerar, e duas que serão completas, então vamos focar na soma dessas duas.
Como no enunciado foi dado
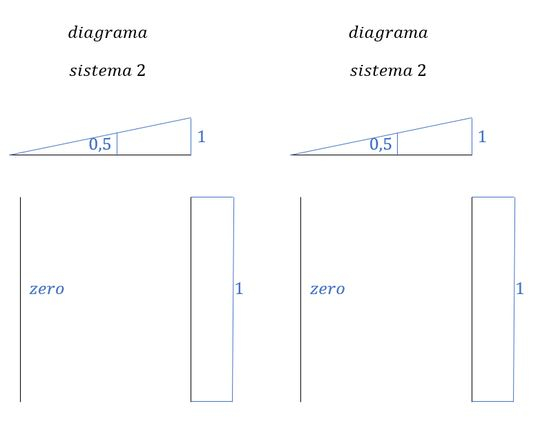
Vemos aqui que temos uma barra que irá zerar, e duas que serão completas, então vamos focar na soma dessas duas.
Como no enunciado foi dado
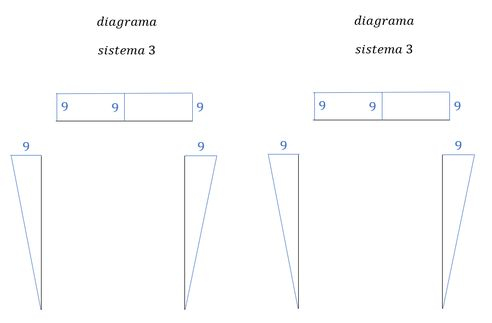
Vemos aqui que temos uma barra que irá zerar, e duas que serão completas, então vamos focar na soma dessas duas.
Como no enunciado foi dado
Vemos que aqui temos duas regiões triangulares, basta que apenas combinemos cada um deles de maneira correta.
Como no enunciado foi dado
Passo 4
Já tendo calculado as deformações, basta substituirmos no nosso sistema que é dado por:
Substituindo:
Passo 5
Agora basta lembrarmos que para termos os esforços no sistema hiperestático devemos usar a relação:
Que significa basicamente
Como queremos a reação de apoio nosso sistema será
E agrupando os sistemas vamos ter que
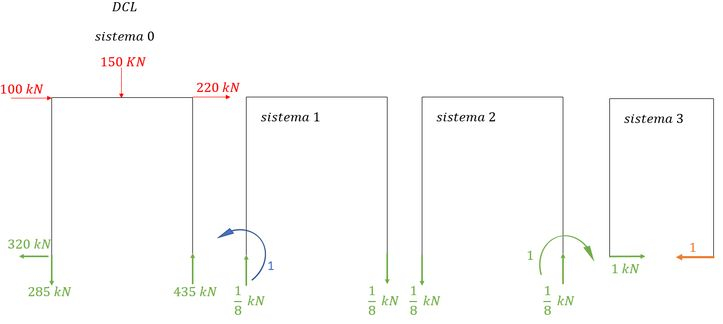
Agora vamos as reações de apoio: