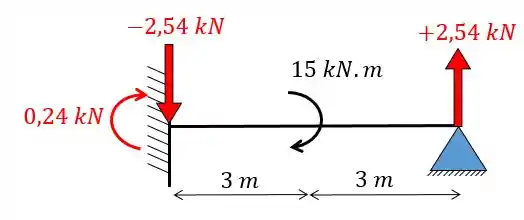
Determine o valor das reações de cada apoio do sistema hiperestático dado abaixo.
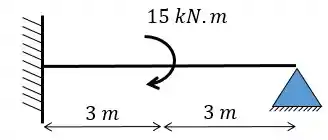
Passo 1
Faaala, galerinha!!! Agora vamos ver como achar as reações de uma viga hiperestática utilizando o método das forças!!!
Para a utilização deste método é muito importante sabermos construir o diagrama de momento fletor e calcular o deslocamento de um ponto numa estrutura isostática.
Então vamos fazer o seguinte:
- Transformar essa estrutura numa estrutura isostática.
- Montar os diagramas de momento fletor.
- Calcular os deslocamentos.
- Achar os hiperestáticos.
- Achar as reações
Passo 2
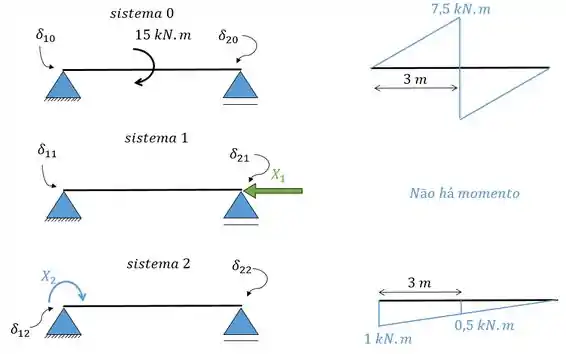
Então vamos transformar nossa viga hiperestática numa viga isostática. Vamos fazer isso transformando o engaste em um apoio de segundo gênero e adicionando um momento; e também transformando o apoio de segundo gênero em apoio do primeiro gênero e adicionando uma força horizontal. Essa força e o momento são os nossos hiperestáticos.
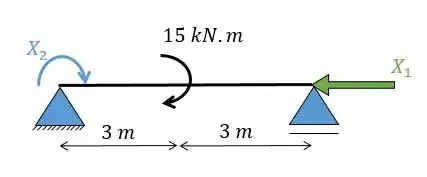
Agora a gente tem que lembrar de separar em sistemas distintos, nesse caso serão três sistemas:
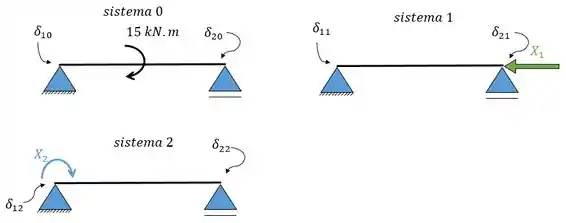
Que nos fornecerão as seguintes equações de deslocamentos.
Passo 3
Agora vamos montar os diagramas de momento fletor para cara sistema lembrando que nosso hiperestático será considerado como uma força ou momento unitário.
Passo 4
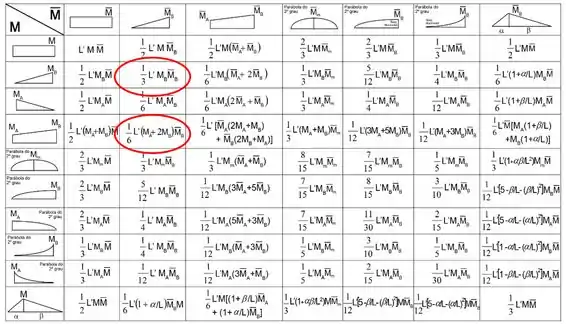
Agora vamos combinar esses diagramas de forma a obter os deslocamentos. Quando eu falo combinar a gente tem que se ligar na seguinte expressão e da tabela
A primeira coisa que a gente pode verificar é que no sistema 1 não há momento logo podemos eliminar todos os deslocamentos que tem 1 como índice, obtendo:
Desta forma o deslocamento pode ser calculado dividindo a viga ao meio e calculando a combinação de um triângulo + trapézio e a combinação de dois triângulos. Lembrando que eles tem sentidos opostos logo temos de adicionar um sinal negativo.
E para vamos ter a combinação de dois triângulos de mesmo sentido:
Passo 5
Com esses dois deslocamentos vamos poder achar o hiperestático :
E o hiperestático ? Pessoal, como o nosso momento fletor deu nulo e não dá pra calcular esse termo então a gente considere ele como sendo zero mesmo beleza?
Passo 6
Agora para achar as reações a gente vai considerar a reação de cada sistema separado:
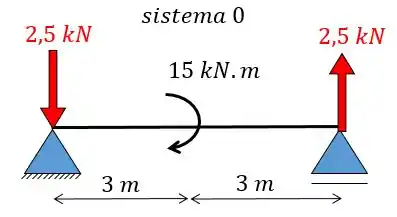
Como o hiperestático é nulo podemos ignorar o sistema 1 e partir para o sistema 2:
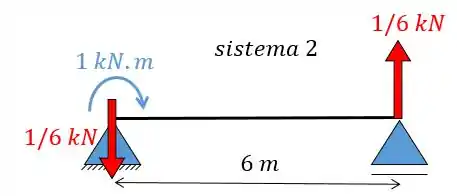
Agora vamos finalmente achar a reação verdadeira:
Para o apoio da esquerda:
Para o apoio da direita:
Passo 7
Para achar as outras reações é só voltar lá no começo e substituir essa reação que acabamos de encontrar e utilizar as equações da estática: