Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Método das forças – Solução dos sistemas de equações e incógnitas

Ver Teoria
Exercício 31245678

Enunciado

Determine o valor das reações de cada apoio do sistema hiperestático dado abaixo.

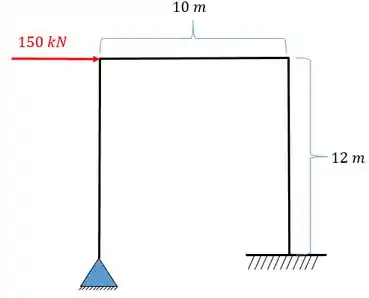
Passo 1

Faaala, galerinha!!! Agora vamos ver como achar as reações de uma viga hiperestática utilizando o método das forças!!!

Para a utilização deste método é muito importante sabermos construir o diagrama de momento fletor e calcular o deslocamento δ de um ponto numa estrutura isostática.

Então vamos fazer o seguinte:

  1. Transformar essa estrutura numa estrutura isostática.
  2. Montar os diagramas de momento fletor.
  3. Calcular os deslocamentos.
  4. Achar os hiperestáticos.
  5. Achar as reações

Passo 2

Para obter uma estrutura isostática vamos fazer o seguinte: retirar o engaste e transformá-lo num apoio de primeiro gênero. Lembre-se que como reduzimos o nosso apoio em dois graus de estabilidade temos de adicionar os respectivos graus como reações. Sendo assim vamos ter o seguinte:

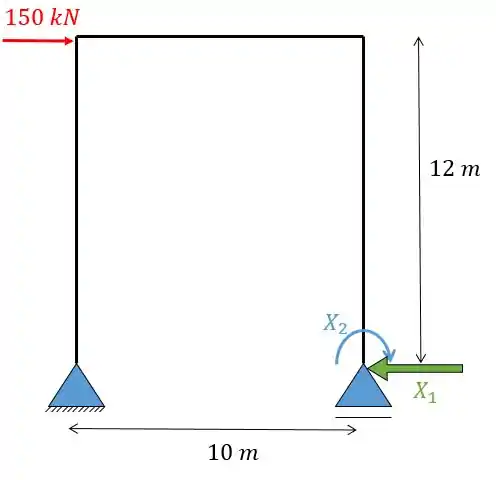
Onde os hiperestáticos são X 1 e X 2 . Colocando em sistemas separados:

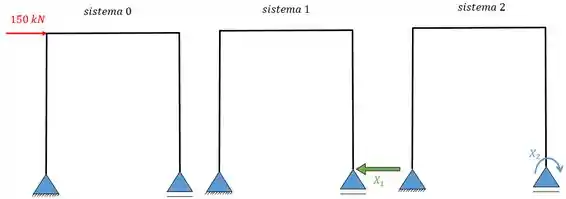
Que fornecerão as seguintes equações:

δ 10 + δ 11 . X 1 + δ 12 . X 2 = 0

δ 20 + δ 21 . X 1 + δ 22 . X 2 = 0

Passo 3

Agora vamos calcular os diagramas dos momentos fletores. Galerinha marota, como o foco da aula não é ficar calculando diagrama eu vou dar de lambuja aqui para vocês mas fiquem espertos que seu prof não vai ser tão bonzinho assim não hein!

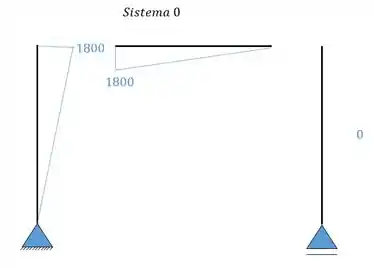
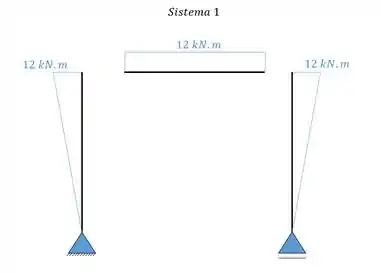
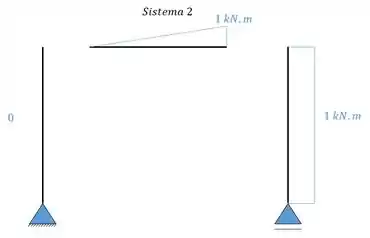
Passo 4

Agora vamos combinar esses diagramas de forma a obter os deslocamentos. Quando eu falo combinar a gente tem que se ligar na seguinte expressão e da tabela

δ 10 + δ 11 . X 1 + δ 12 . X 2 = 0

δ 20 + δ 21 . X 1 + δ 22 . X 2 = 0

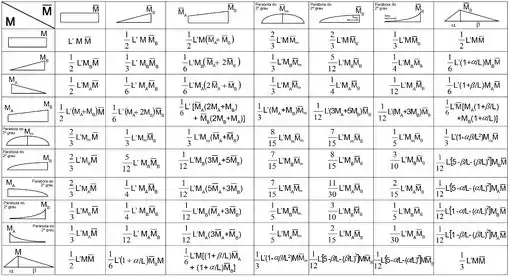
Agora vamos para as combinações afim de calcular os deslocamentos. Começando por δ 10 que é a composição entre o sistema 1 e o sistema 0. Para δ 10 vamos ter duas combinações: uma entre dois triângulos e outra entre um retângulo e um triângulo:

E J δ 10 = - 1 3 L ' M M - - 1 2 L ' . M . M -

E J δ 10 = - 1 3 12 1800 12 - 1 2 10 . 1800 . ( 12 )

δ 10 = - 194400 E J

Para δ 11 vamos ter:

E J δ 11 = 1 3 L ' M M - + L ' M M - + 1 3 L ' M M -

E J δ 11 = 1 3 12 12 12 + 10 12 12 + 1 3 ( 12 ) ( 12 ) ( 12 )

δ 11 = 2592 E J

Para δ 12 vamos ter:

E J δ 12 = 1 2 L ' . M . M - + 1 2 L ' . M . M -

E J δ 12 = 1 2 ( 10 ) . ( 12 ) . ( 1 ) + 1 2 ( 12 ) . ( 1 ) . ( 12 )

δ 12 = 132 E J

Para δ 20 vamos ter:

E J δ 20 = - 1 6 L ' . M . M -

E J δ 20 = - 1 6 . ( 10 ) ( 1800 ) ( 1 )

δ 20 = - 3 000 E J

Para δ 21

δ 21 = δ 12

Rá rá!! Gostou né? Quando eles são opostos assim eles são iguais!

δ 22 = 1 3 L ' M M - + L ' M M -

E J δ 22 = 1 3 ( 10 ) ( 1 ) ( 1 ) + ( 12 ) ( 1 ) ( 1 )

δ 22 = 15,33 E J

Passo 5

Agora a gente resolve a equação para achar X 1 e X 2

δ 10 + δ 11 . X 1 + δ 12 . X 2 = 0

δ 20 + δ 21 . X 1 + δ 22 . X 2 = 0

Substituindo

- 194400 E J + 2592 E J . X 1 + 132 E J . X 2 = 0

- 3 000 E J + 132 E J . X 1 + 15,33 E J . X 2 = 0

Nós podemos simplificar tudo por E J

- 194400 + 2592 . X 1 + 132 . X 2 = 0

- 3000 + 132 . X 1 + 15,33 . X 2 = 0

X 1 = 115,8

X 2 = - 801,6

Passo 6

Agora para achar as reações a gente vai considerar a reação de cada sistema separado:

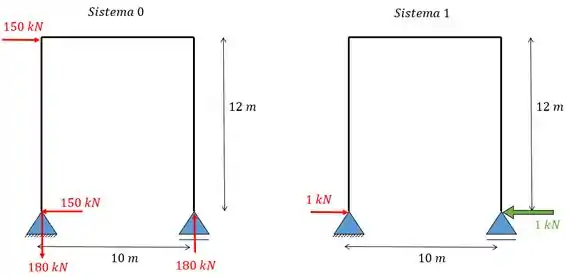
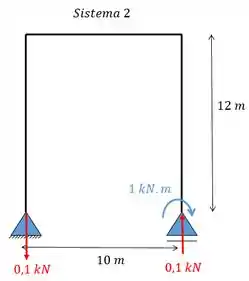
Agora podemos achar a reação verdadeira. Para o apoio da esquerda vamos ter:

R v = R v 0 + R v 1 . X 1 + R v 2 . X 2

R v = - 180 + 0 + 0,1   . -   801.6 = - 260,16   k N

Para o apoio da direita vamos ter o contrário:

R v = 260,16   k N

A reação horizontal no apoio da esquerda é:

R H = R H 0 + R H 1 . X 1 + R H 2 . X 2

R H = - 150 + 1   .   115,8 = - 34,2   k N

Já no apoio da esquerda é

R H = - 150 - 34,2 = - 184,2   k N

E para achar o momento no apoio da direita, que é engastado, vamos olhar os momentos lá nos diagramas dos 3 sistemas:

M = M 0 + M 1 X 1 + M 2 X 2

M = 0 + 0 + 1   .   - 801,6 = - 801,6   k N m

Resposta

No apoio da esquerda:

R v = - 260,16   k N

R H = - 34,2   k N

No apoio da direita:

R v = 260,16   k N

R H = - 184,2   k N

M = - 801,6   k N m