Resolva o sistema de oscilações
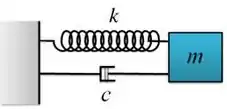
Passo 1
Vamos usar a segunda lei de Newton para conseguir montar a equação diferencial.
Mas para isso precisamos fazer o diagrama de forças atuantes. Fica assim:
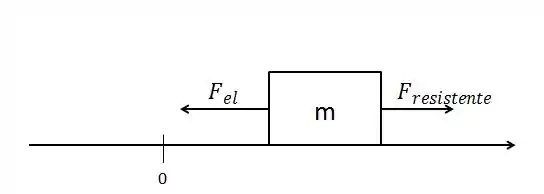
Passo 2
Temos:
Então, pela segunda lei de Newton, a força resultante é dada pela soma de todas as forças atuantes:
Porém:
Temos:
Que equivale a:
Ajeitando:
Vamos usar o seguinte:
Então a EDO fica:
Passo 3
E como é que a gente resolve?
Quando temos uma EDO de 2ª ordem homogênea, resolvemos a equação auxiliar:
Assim:
Onde
Viu porque ele substituiu por Nego não ta de zoeira não! Cortou muita coisa
E então temos três possibilidades:
Em cada caso, temos uma solução diferente, lembra?
Então vamos analisar cada uma dessas possibilidades agora.
Mas antes vamos dar nome aos bois, mas relaxa com isso, é só para você entender o que tá acontecendo, esse tipo de nomenclatura não é cobrado na sua prova!
Quando : amortecimento subcrítico;
Quando : amortecimento crítico;
Quando : amortecimento supercrítico;
É só você lembrar que “sub” significa “abaixo” (abaixo de zero) e “super” significa “acima” (acima de zero).
Beleza?
Então vamos lá!
Passo 4
Passo 5
Nesse caso:
Então a equação auxiliar tem duas raízes reais e distintas:
E a solução é dada por:
As constantes e são dadas pelas condições iniciais de e .
O gráfico do amortecimento supercrítico tem essa cara(Só por curiosidade):

Uma soma de exponenciais decrescentes.
Passo 6
Nesse caso:
Então a equação auxiliar tem duas raízes reais e iguais:
E a solução é dada por:
Ou, se preferir colocar em evidência:
As constantes e também são dadas pelas condições iniciais de e .
E o gráfico do amortecimento crítico tem mais ou menos a mesma cara do amortecimento supercrítico(Isso é só por curiosidade!):

Passo 7
Nesse caso:
Então a equação auxiliar tem duas raízes imaginárias:
E a solução é dada por:
As constantes e são sempre dadas pelas condições iniciais de e .
E o gráfico do amortecimento subcrítico tem uma cara assim(Só por curiosidade again!!):
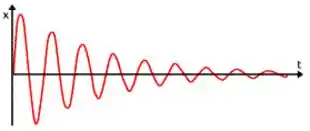
Nesse caso, o movimento é oscilatório, mas as amplitudes vão sendo cada vez menores, até parar.
Resposta
ou
ou
Depende da relação entre e !(Para saber se