Um voltímetro, mostrado na figura abaixo, possui um ponteiro de alumínio de comprimento , largura , e espessura . A mola restauradora tem uma constante de mola rotacional . Um amortecedor para amortecimento crítico é posicionado a um raio . Durante uma medida, o instrumento mostra . Quando a voltagem é desligada, determinar o tempo requerido para o ponteiro retornar à indicação de .
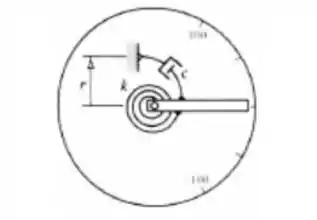
Passo 1
Antes de a gente começar, vou te dar algumas sugestões aqui, a final de contas, o nosso interesse é calcular uma EDO e não ficar procurando Momento de inércia de ponteiro (paralelepípedo), não é mesmo?
- Primeiro, vamos considerar o problema angular, onde o ângulo que o ponteiro faz com a horizontal depende do tempo : .
- Segundo, que se o problema é angular, então trabalhemos com torques!
- O Torque da força peso do ponteiro é , onde...
- E, caso precise, a velocidade do ponteiro, é de .
AHHH! Grande coisa! Mudou a minha vida saber disso!

Se você está agora como a Nazaré, então me siga !
Passo 2
Já vou te adiantando que esse exercício não é brincadeira, mas ao mesmo tempo é um problema de se apaixonar!
Para começar, vamos entender o que a gente busca no problema, ok?
Como o enunciado nos deu um valor inicial de medida (), trata-se de um problema de valor inicial, onde estamos buscando o tempo necessário para agulha retornar para a posição de desligado. Ora, a palavra chave desse problema, está em:
“Um amortecedor para amortecimento crítico é posicionado”
Essa é uma expressão fundamental, porque se você recordar na teoria, amortecimentos críticos, caso estivermos falando de uma EDO de ordem, possuem uma equação dessa forma aqui:
Ora! Nós temos o tempo inicial quando medimos , falta encontrarmos o tempo final . Daí, o tempo para o ponteiro retornar à indicação de será , o valor buscado no problema!
AHA! Então isso significa que estamos no caminho certo! Mas infelizmente, essa expressão só funciona, caso estivermos falando de uma modelagem envolvendo equações diferenciais de ordem. Então para responder o problema, precisamos averiguar as respostas para essas perguntinhas aqui:
- A modelagem é uma equação de ordem? Se for, quem ela é?
- Quem é e ?
- Quem é ?
Após essas perguntas, é fácil encontrar , bastando substituir!
Passo 3
Primeiro vamos responder a primeira e uma das mais importantes perguntas da rodada: A modelagem é uma equação de ordem? Se for, quem ela é? É com essa pergunta, que vãos (vamos) de fato averiguar se a equação do amortecimento acima pode ser usada.
O problema que estamos lidando, é um problema regido pela mecânica Newtoniana. Então vamos começar listando os torques envolvidos no problema:
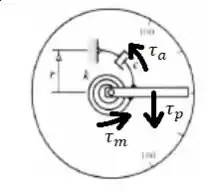
- Temos o torque causado pela força peso do ponteiro .
- Temos o Torque causado pela mola .
- E temos o Torque causado pela força de amortecimento .
De acordo com a Lei de Newton, o torque resultante é a soma dos outros dois, para o sistema entrar em equilíbrio:
, de acordo com a sugestão, é dado por:
Onde:
é o momento de inércia do ponteiro:
é a aceleração angular:
, por sua vez, é dado por:
(OBS de física: esse é a constante de mola rotacional, portanto vezes o deslocamento angular já é o torque, diferentemente de , onde esse não é rotacional, então o produto nos dá a força).
Enquanto isso, :
Onde:
é a constante de amortecimento;
é a velocidade do ponteiro, dado por .
Juntando tudo na expressão Newtoniana de torque resultante:
Simplificando um pouco...
Pelo enunciado, sabemos que:
Então...
Agora é só simplificação, veja:
Ou...
Veja que de fato a modelagem é uma EDO de segunda ordem!
Passo 4
Com isso, estamos prontos para responder a segunda pergunta: Quem é e ?
Sabemos que a resposta dessa equação, devido ao fato de estarmos trabalhando com um amortecimento crítico, será da forma:
Sabemos também, que a tensão no tempo inicial é . Mas agora, que ângulo isso corresponde?
Pela posição no desenho,
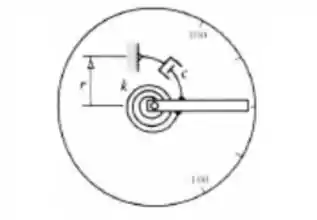
é . Agora não tem como de saber, neh? Na verdade, também não é tão relevante assim. Então se chamarmos de um ângulo de , onde um ângulo qualquer que a gente não conhece, então com uma regrinha de 3, o ângulo correspondente a ...
(No final das contas, o que está valendo é a proporção, está vendo?)
Sabemos também que por se tratar de uma equação de segunda ordem, temos que ter a velocidade no tempo inicial! Como no tempo inicial, o ponteiro estava parado, então...
Essas são as condições iniciais:
Passo 5
Descobrindo substituindo a primeira condição na equação...
Como ...
Logo...
Passo 6
Descobrindo usando a segunda condição . Logo a gente precisa derivar a equação...
Substituindo tudo o que conhecemos...
Logo...
Ou
Estamos prontos agora para descobrir quem é ...
Passo 7
A última pergunta (quem é ?) pode ser respondida lembrando que é a frequência de oscilação sem amortecimento, pode ser obtida através da equação de modelagem do sistema assim:
Então, a nossa equação de amortecimento crítico final é...
Passo 8
Só falta então, finalmente encontrarmos o tempo final comentado lá no passo para fecharmos o problema com chave de ouro:
Sabemos que no tempo final , temos a tensão de , em termos de ângulo, isso quer dizer . Logo,
Com um auxílio de uma calculadora a gente descobre que então esse é o tempo que a agulha demora a retornar ao ponto inicial!
Eu sei! Foi um problema grande e que necessitou da calculadora em vários momentos, mas vai falar que não é um problema elegante? :D
AH! E só mais uma coisa, esse é um problema de mecânica, por isso se isso cair na sua prova de cálculo, não se preocupe! O seu professor vai te dar aquelas sugestões como nós demos aqui, afinal, você não é obrigado a se lembrar de momento de inércia de um ponteiro (paralelepípedo) !