Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos elétricos

Ver Teoria
Exercício 31245678

Enunciado

Determine a função de transferência V S ( s ) / V ( s ) para o circuito abaixo:

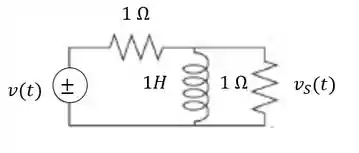
Passo 1

Vamos usar a lei das malhas para resolver esse. A lei das malhas diz que a soma das tensões em uma determinada malha é igual a 0 .

Temos aqui um circuito com duas malhas, vamos desenhar para conseguir ver melhor:

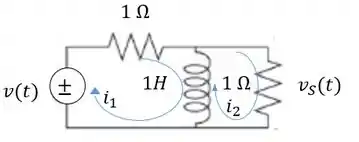
Passo 2

Vamos escrever uma equação para cada malha usando a lei das malhas, para isso, devemos escrever a tensão em todos os elementos de cada malha.Vamos usar essa tabela para nos auxiiar:

Para a primeira malha:

v t - R i 1 - L d i 1 t d t + L d i 2 d t = 0

Substituindo os valores dados:

v t - i 1 - d i 1 t d t + d i 2 t d t = 0

v t = i 1 t + d i 1 t d t - d i 2 t d t                 ( 1 )

Para a segunda malha:

- L d i 2 t d t + L d i 1 t d t - R i 2 ( t ) = 0

0 = i 2 ( t ) + d i 2 ( t ) d t - d i 1 t d t           ( 2 )

Passo 3

O próximo passo é aplicar Laplace, para que possamos manipular nossas equações mais facilmente.

Aplicando Laplace em ( 1 ) e ( 2 ) :

V s = I 1 s + s I 1 s - s I 2 s = s + 1 I 1 s - s I 2 s         ( 3 )

0 = I 2 s + s I 2 s - s I 1 s = 1 + s I 2 s - s I 1 ( s )           ( 4 )

Vamos agora isolar I 1 s em ( 4 ) :

I 1 s = s + 1 s I 2 ( s )

Substituindo em ( 3 ) :

V s = s + 1 s + 1 s I 2 s - s I 2 ( s )

V s = s + 1 s + 1 s - s I 2 ( s )

V s = 2 s + 1 s I 2 s                 ( 5 )

Passo 4

Entretanto, o exercício pede que a gente calcule V S s V s , que é a relação entre a tensão no resistor e a tensão de entrada do circuito.

A tensão no resistor pode ser calculada como:

v S t = R i 2 t = i 2 ( t )

Aplicando Laplace:

V S s = I 2 ( s )

Substituindo em ( 5 ) :

V s = 2 s + 1 s V S s

Por fim:

V S s V s = s 2 s + 1

Resposta

V S s V s = s 2 s + 1