Determine a função de transferência para o circuito passivo abaixo:
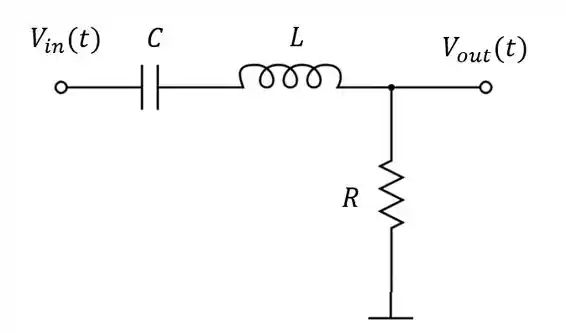
Passo 1
Vamos resolver esse circuito pela regra dos nós. Como temos apenas um nó no circuito, a gente já sabe em qual aplicar a regra.
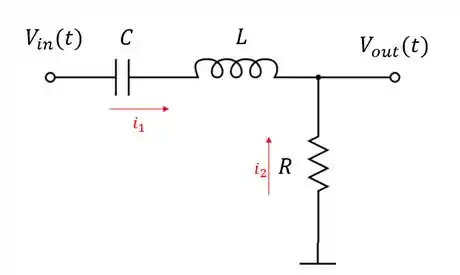
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
Precisaremos, então, encontrar as corrente e para aplicar a regra dos nós. Entretanto, a corrente passa por um capacitor e um indutor. Para encontrar essa corrente em função de e , precisaremos determinar um ponto intermediário:
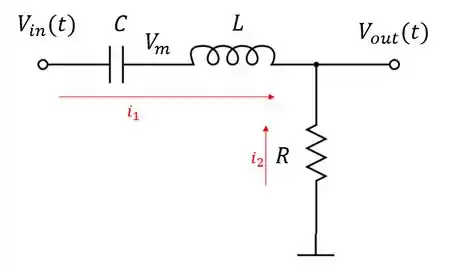
Vamos então definir duas expressões para . Como a corrente que passa pelo capacitor e indutor é a mesma, podemos escrever uma expressão para cada elemento:
Precisamos isolar em uma das expressões e substituir na outra, entretanto, por se tratar de equações diferenciais, essa manipulação vai ficar mais fácil se aplicarmos Laplace:
Vamos isolar em :
Substituindo em :
Isolando :
Ufa, finalmemte conseguimos uma expressão para que relaciona e
Passo 3
A expressão para é mais fácil de obter:
Esse zdro aí em cima é devido ao fato do ramo de onde “vem” a estar aterrado, logo, a tensão é .
Aplicando Laplace:
Passo 4
Por fim, somando-se as duas corresntes:
Rearranjando:
Simplificando: