Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos elétricos

Ver Teoria
Exercício 21345678

Enunciado

Determine a função de transferência para o circuito passivo abaixo:

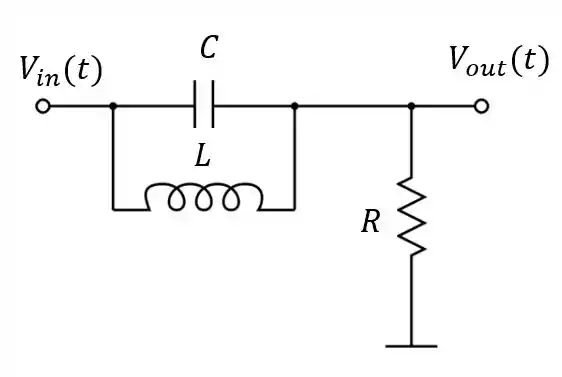
Passo 1

Vamos resolver esse circuito pela regra dos nós. O nó destacado abaixo é o que está na posição mais estratégica da malha, então, vamos usá-lo como referância

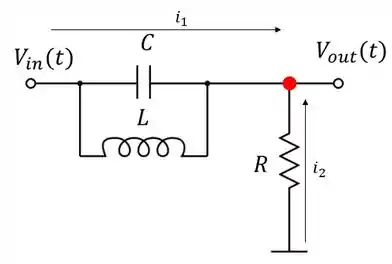
Logo:

i 1 + i 2 = 0

Obs: a direção das setas é arbitrado.

Passo 2

Para a corrente i 1 , temos um capacitor e um indutor em paralelo. Logo a corrente i 1 é a soma das correntes que passam no insutor e no capacitor:

i 1 t = i L + i C

i 1 t = 1 L ∫ V o u t t - V i n t d t + C d V o u t t - V i n t d t

A corrente i 2 é proveniente de um ramo que contém um resistor e está aterrada, logo:

i 2 t = V o u t t R

Juntando tudo:

i 1 + i 2 = 0

1 L ∫ V o u t t - V i n t d t + C d V o u t t - V i n t d t + V o u t t R = 0

Passo 3

Agora que já temos nossa EDO, basta aplicar Laplace:

1 L s V o u t s - V i n s + C s V o u t s - V i n s + V o u t s R = 0

Rearranjando:

1 L s V o u t s + C s V o u t s + V o u t R = 1 L s V i n s + C s V i n s

1 L s + C s + 1 R V o u t s = 1 L s + C s V i n

V o u t s V i n s = 1 L s + C s 1 L s + C s + 1 R

Simplificando:

V o u t s V i n s = R + R L C s 2 R + R L C s 2 + L s

Resposta

V o u t s V i n s = R + R L C s 2 R + R L C s 2 + L s