Determine a função de transferência para o circuito passivo abaixo:
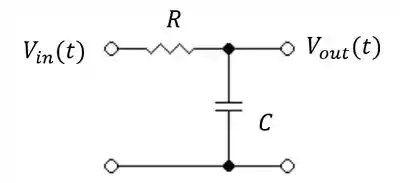
Passo 1
Para modelar circuitos elétricos devemos utilizar sempre a lei das malhas ou a lei dos nós. Como nesse caso não temos nenhuma malha fechada, vamos usar a lei dos nós.
A lei dos nós diz que a soma de todas as correntes chegando em nó é igual à soma de todas as correntes saindo desse nó.
Vamos desenhar isso:
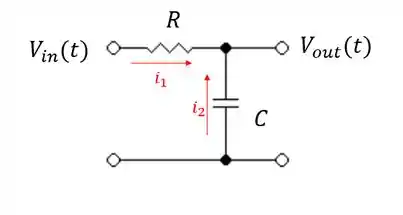
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
Para calcular a corrente devemos ver de onde ela está vindo. A corrente vem de um resistor, e para um resistor temos que:
Esse é a diferença de tensão, sendo assim:
A corrente vem de um capacitor. Para o capacitor temos que:
Como antes do capacitor não temos nenhuma tensão:
Sendo assim, nossa EDO ficará:
Passo 3
Agora que já temos a nossa EDO, só precisamos aplicar Laplace e depois reorganizar para conseguir a função de transferência.
Aplicando Laplace em :
Reorganizando:
Por fim:
Ou: