Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Modelos elétricos

Ver Teoria
Exercício 51234678

Enunciado

Determine a função de transferência V S ( s ) / V ( s ) para o circuito abaixo:

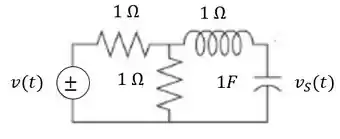
Passo 1

Vamos resolver esse exercício aplicando a lei das malhas para o circuito, sendo assim, a soma de todas as tensões dentro de uma malha deve ser igual a 0 .

Vamos considerar as duas malhas internas do circuito representadas abaixo pelas correntes i 1 e i 2 .

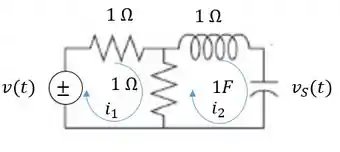
Passo 2

Devemos escrever então duas equações, uma pra cada malha. Devemos somar todas as tensões presentes em cada malha. Para isso, usaremos as fómulas da tabela:

Para a primeira malha:

v t = i 1 t + i 1 t - i 2 t = 2 i 1 t - i 2 ( t )           ( 1 )

Para a segunda malha:

0 = d i 2 t d t + ∫ i 2 t d t + i 2 ( t ) - i 1 t                   ( 2 )

Passo 3

Como trabalhar com um sistema de EDO’s é uma coisa muito complicada e nada prática, vamos aplicar Laplace para facilitar nossas manipulações.

Aplicando Laplace em ( 1 ) :

V s = 2 I 1 s - I 2 s

V s = 4 + 2 s I 1 s - 2 + 1 s I 2 s                     ( 3 )

Agora em ( 2 ) :

0 = s I 2 s + I 2 s s + I 2 s - I 1 ( s )

Isolando I 1 ( s )

I 1 s = s + 1 s + 1 I 2 s               ( 4 )

Substituindo ( 4 ) em ( 3 ) :

V s = 2 s + 1 s + 1 I 2 s - I 2 ( s )

V s = 2 s + 2 s + 1 I 2 s                   ( 5 )

Passo 4

Entretanto, o exercício pede a relação entre a tenção no indutor e a tensão de entrada do circuito.

A tensão no indutor pode ser calculada como:

v S t = 1 C ∫ i 2 t d t = ∫ i 2 t d t

Aplicando Laplace:

V S s = I 2 s s

Logo:

I 2 s = s V S s

Substituindo em ( 5 ) :

V s = 2 s + 2 s + 1 s V S s

V s = 2 s 2 + s + 2 V S ( s )

Por fim:

V S s V s = 1 2 s 2 + s + 2

Resposta

V S s V s = 1 2 s 2 + s + 2