Determine a função de transferência para o circuito passivo abaixo:
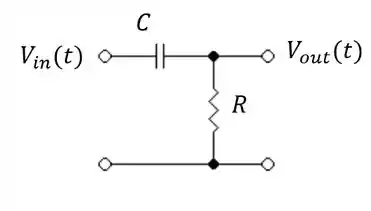
Passo 1
Como não temos uma malha clara nesse circuito, fica mais fácil encontrar a função de transferência pela lei dos nós.
A lei dos nós diz que a soma das correntes que chega em um nó é igual a .
Vamos considerara o nó de cima para fazer as contas. Sendo assim:
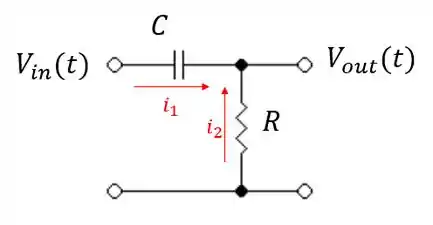
Logo:
Obs: a direção das setas é arbitrado.
Passo 2
A corrente vem de uma “linha” onde existe um capacitor. Sendo assim:
Sendo assim, para o nosso circuito
A corrente vem de um resistor. Para o capacitor temos que:
Antes do resistor não existe nenhum componente, portanto, não existe tensão:
Sendo assim, nossa EDO ficará:
Passo 3
O próximo passo depois que a gente obtem a EDO para conseguir a função de transferência é a aplicação da transformada de Laplace.
Aplicando Laplace em :
Reorganizando:
Por fim:
Ou:
Obs: se você ainda tem dúvida em transformada de Laplace, seria legal dar uma revisada nesse tópico porque ele é muito importante para nós em controle de processo.